题目内容
 已知焦点在x轴上的椭圆C过点(0,1),且离心率为
已知焦点在x轴上的椭圆C过点(0,1),且离心率为 ,Q为椭圆C的左顶点.
,Q为椭圆C的左顶点.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知过点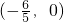 的直线l与椭圆C交于A,B两点.
的直线l与椭圆C交于A,B两点.
(ⅰ)若直线l垂直于x轴,求∠AQB的大小;
(ⅱ)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.
解:(Ⅰ)设椭圆C的标准方程为 (a>b>0),且a2=b2+c2.
(a>b>0),且a2=b2+c2.
由题意,椭圆C过点(0,1),离心率为 ,可知:b=1,
,可知:b=1, =
= .…(2分)
.…(2分)
所以a2=4.
所以,椭圆C的标准方程为 .…(3分)
.…(3分)
(Ⅱ)由(Ⅰ)得Q(-2,0).设A(x1,y1),B(x2,y2).
(ⅰ)当直线l垂直于x轴时,直线l的方程为x=- .
.
由 ,解得
,解得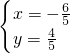
即A(- ,
, ),B(-
),B(- ,-
,- )(不妨设点A在x轴上方).…(5分)
)(不妨设点A在x轴上方).…(5分)
则直线AQ的斜率1,直线BQ的斜率-1.
因为直线AQ的斜率与直线BQ的斜率为-1,所以AQ⊥BQ,所以∠AQB= .…(6分)
.…(6分)
(ⅱ)当直线l与x轴不垂直时,由题意可设直线AB的方程为y=k(x+ )(k≠0).
)(k≠0).
由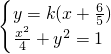 消去y得:(25+100k2)x2+240k2x+144k2-100=0.
消去y得:(25+100k2)x2+240k2x+144k2-100=0.
因为点A(- ,0)在椭圆C的内部,显然△>0.
,0)在椭圆C的内部,显然△>0.
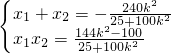 …(8分)
…(8分)
因为 =(x1+2,y1),
=(x1+2,y1),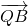 =(x2+2,y2),y1=k(x1+
=(x2+2,y2),y1=k(x1+ ),y2=k(x2+
),y2=k(x2+ ),
),
所以 •
•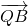 =(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+
=(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+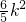 )(x1+x2)+4+
)(x1+x2)+4+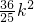
=(1+k2)×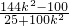 +(2+
+(2+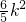 )(
)(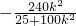 )+4+
)+4+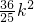 =0
=0
所以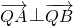 .
.
所以△QAB为直角三角形.…(11分)
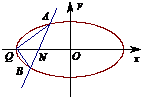 假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|.
假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|.
取AB的中点M,连接QM,则QM⊥AB.
记点(- ,0)为N.
,0)为N.
另一方面,点M的横坐标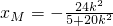 ,
,
所以点M的纵坐标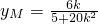 .
.
所以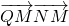 =(
=( )•(
)•(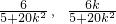 )=
)=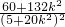 ≠0
≠0
所以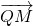 与
与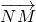 不垂直,矛盾.
不垂直,矛盾.
所以当直线l与x轴不垂直时,不存在直线l使得△QAB为等腰三角形.…(13分)
分析:(Ⅰ)设椭圆C的标准方程为 (a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为
(a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为 ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;
(Ⅱ)由(Ⅰ)得Q(-2,0).设A(x1,y1),B(x2,y2).
(ⅰ)当直线l垂直于x轴时,直线l的方程为x=- ,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小;
,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小;
(ⅱ)当直线l与x轴不垂直时,设直线AB的方程为y=k(x+ )(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算
)(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算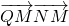 ,即可得到结论.
,即可得到结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,解题的关键是直线与椭圆联立,利用韦达定理进行求解.
 (a>b>0),且a2=b2+c2.
(a>b>0),且a2=b2+c2.由题意,椭圆C过点(0,1),离心率为
 ,可知:b=1,
,可知:b=1, =
= .…(2分)
.…(2分)所以a2=4.
所以,椭圆C的标准方程为
 .…(3分)
.…(3分)(Ⅱ)由(Ⅰ)得Q(-2,0).设A(x1,y1),B(x2,y2).
(ⅰ)当直线l垂直于x轴时,直线l的方程为x=-
 .
.由
 ,解得
,解得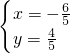
即A(-
 ,
, ),B(-
),B(- ,-
,- )(不妨设点A在x轴上方).…(5分)
)(不妨设点A在x轴上方).…(5分)则直线AQ的斜率1,直线BQ的斜率-1.
因为直线AQ的斜率与直线BQ的斜率为-1,所以AQ⊥BQ,所以∠AQB=
 .…(6分)
.…(6分)(ⅱ)当直线l与x轴不垂直时,由题意可设直线AB的方程为y=k(x+
 )(k≠0).
)(k≠0).由
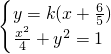 消去y得:(25+100k2)x2+240k2x+144k2-100=0.
消去y得:(25+100k2)x2+240k2x+144k2-100=0.因为点A(-
 ,0)在椭圆C的内部,显然△>0.
,0)在椭圆C的内部,显然△>0.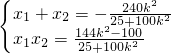 …(8分)
…(8分)因为
 =(x1+2,y1),
=(x1+2,y1),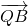 =(x2+2,y2),y1=k(x1+
=(x2+2,y2),y1=k(x1+ ),y2=k(x2+
),y2=k(x2+ ),
),所以
 •
•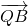 =(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+
=(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+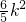 )(x1+x2)+4+
)(x1+x2)+4+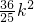
=(1+k2)×
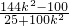 +(2+
+(2+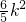 )(
)(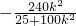 )+4+
)+4+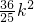 =0
=0所以
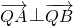 .
.所以△QAB为直角三角形.…(11分)
 假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|.
假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|.取AB的中点M,连接QM,则QM⊥AB.
记点(-
 ,0)为N.
,0)为N.另一方面,点M的横坐标
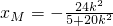 ,
,所以点M的纵坐标
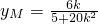 .
.所以
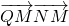 =(
=( )•(
)•(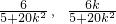 )=
)=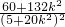 ≠0
≠0所以
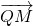 与
与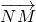 不垂直,矛盾.
不垂直,矛盾.所以当直线l与x轴不垂直时,不存在直线l使得△QAB为等腰三角形.…(13分)
分析:(Ⅰ)设椭圆C的标准方程为
 (a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为
(a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为 ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;(Ⅱ)由(Ⅰ)得Q(-2,0).设A(x1,y1),B(x2,y2).
(ⅰ)当直线l垂直于x轴时,直线l的方程为x=-
 ,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小;
,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小;(ⅱ)当直线l与x轴不垂直时,设直线AB的方程为y=k(x+
 )(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算
)(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算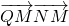 ,即可得到结论.
,即可得到结论.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,解题的关键是直线与椭圆联立,利用韦达定理进行求解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( ) 和椭圆弧
和椭圆弧
