题目内容
已知函数![]() 的定义域为
的定义域为![]() 。
。
(1)求证:直线![]() (其中
(其中![]() )不是函数
)不是函数![]() 图像的切线;
图像的切线;
(2)判断![]() 在
在![]() 上单调性,并证明;
上单调性,并证明;
(3)已知常数![]() 满足
满足![]() ,求关于
,求关于![]() 的不等式
的不等式![]() 的解集
的解集
(1)见解析(2)![]() 在
在![]() 上是减函数
上是减函数
(3)当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()
当![]() 时,原不等式解集为Φ
时,原不等式解集为Φ
当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()
解析:
(1)![]() 2分
2分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 而
而![]() 在
在![]() 连续,∴
连续,∴![]() 在
在![]() 上是减函数,又
上是减函数,又![]()
∴函数![]() 图像上任意点处切线斜率
图像上任意点处切线斜率![]() 存在并满足
存在并满足![]() 4分
4分
当![]() 时,直线
时,直线![]() 斜率不存在,∴直线
斜率不存在,∴直线![]() 不是函数
不是函数![]() 图像的切线;当
图像的切线;当![]() 时,直线
时,直线![]() 斜率
斜率![]() ,则
,则![]() ,∴直线
,∴直线![]() 不是函数
不是函数![]() 图像的切线 6分
图像的切线 6分
已知函数![]() 的定义域为
的定义域为![]() 。
。
(2)由(1)易知![]() 在
在![]() 上是减函数,而
上是减函数,而![]() ,当
,当![]() 时,
时,![]() ,而
,而![]() 在
在![]() 上连续,∴
上连续,∴![]() 在
在![]() 上是减函数 10分
上是减函数 10分
(3)∵![]() 在
在![]() 上是减函数,并且
上是减函数,并且![]() 在
在![]() 上是偶函数
上是偶函数
由不等式![]()
等价于![]()
∵![]() ,
,![]()
∴![]() ,
,
即![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()
当![]() 时,原不等式解集为Φ
时,原不等式解集为Φ
当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为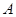 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.