摘要：求证:(利用等差数列求和公式推导)
网址：http://m.1010jiajiao.com/timu3_id_4469753[举报]
已知
为数列
的前
项和，
，
.
⑴设数列
中，
，求证：是等比数列；
⑵设数列
中，
，求证：是等差数列；
⑶求数列的通项公式及前项和.
【解题思路】由于和中的项与中的项有关，且
，可利用
、的关系作为切入点.
已知函数F（x）=
(x≠
)．
（I）求F（
）+F（
）+…+F（
）；
（II）已知数列{an}满足a1=2，an+1=F（an），证明{
}为等差数列（n∈N*），并求数列{an}的通项公式；
（III）已知若b＞a＞0，c＞0，则必有
＞
，利用此结论，求证：a1a2…an＞
（n∈N*）．
查看习题详情和答案>>
| 3x-2 |
| 2x-1 |
| 1 |
| 2 |
（I）求F（
| 1 |
| 2011 |
| 2 |
| 2011 |
| 2010 |
| 2011 |
（II）已知数列{an}满足a1=2，an+1=F（an），证明{
| 1 |
| an-1 |
（III）已知若b＞a＞0，c＞0，则必有
| b |
| a |
| b+c |
| a+c |
| 2n+1 |
．
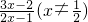）+F（
）+…+F（
）；
}为等差数列（n∈N*），并求数列{an}的通项公式；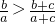
，利用此结论，求证：a1a2…an＞
（n∈N*）．
(x≠
)．
)＋F(
)＋…＋F(
)；
}为等差数列(n∈N*)，并求数列{an}的通项公式；
＞
，利用此结论，求证：a1a2…an＞
(n∈N*)．