题目内容
已知![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,
,![]() .
.
⑴设数列![]() 中,
中,![]() ,求证:
,求证:![]() 是等比数列;
是等比数列;
⑵设数列![]() 中,
中,![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
⑶求数列![]() 的通项公式及前
的通项公式及前![]() 项和.
项和.
【解题思路】由于![]() 和
和![]() 中的项与
中的项与![]() 中的项有关,且
中的项有关,且![]() ,可利用
,可利用![]() 、
、![]() 的关系作为切入点.
的关系作为切入点.
⑴证明略⑵证明略⑶![]()
解析:
⑴![]()
![]() ,
,![]()
![]() ,两式相减,得
,两式相减,得
![]() ,
,![]()
![]()
又![]()
![]() ,
,![]()
![]() ,由
,由![]() ,
,![]() ,得
,得 ![]()
![]()
![]() ,
,![]()
![]() 是等比数列,
是等比数列,![]() .
.
⑵由⑴知,![]() ,且
,且![]()
![]()
![]()
![]()
![]() 是等差数列,
是等差数列,![]() .
.
⑶![]()
![]() ,且
,且![]() ,
,![]()
![]()
当![]() 时,
时,![]() ,
,
![]()
![]() ,
,![]()
【名师指引】⑴等差、等比数列的证明方法主要有定义法、中项法;⑵将“![]() ”化归为
”化归为
![]() 是解题的关键.
是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
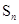 为数列
为数列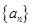 的前
的前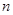 项和,且
项和,且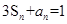 ,数列
,数列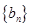 满足
满足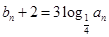 ,数列
,数列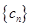 满足
满足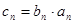 .
. .
.