摘要：21．如图.已知线段|AB|=4.动圆与线段AB切于点C.且|AC|-|BC|=2.过点A.B分别作⊙的切线.两切线相交于P.且P.均在AB的同侧. ⑴建立适当坐标系.当位置变化时.求动点P的轨迹E的方程, ⑵过点B作直线交曲线E于点M.N.求△AMN的面积的最小值.
网址：http://m.1010jiajiao.com/timu3_id_4452946[举报]
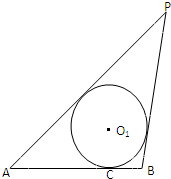如图：已知线段AB=4，动圆O1与线段AB相切于点C，且AC-BC=2| 2 |
（Ⅰ）建立适当坐标系，当O1位置变化时，求动点P的轨迹E方程；
（Ⅱ）过点B作直线交曲线E于点M、N，求△AMN面积的最小值．
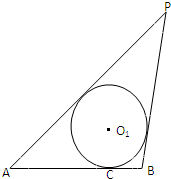
如图：已知线段AB=4，动圆O1与线段AB相切于点C，且AC-BC=2
，过点A，B分别作⊙O1的切线，两切线相交于点P，且P、O1均在AB的同侧．
（Ⅰ）建立适当坐标系，当O1位置变化时，求动点P的轨迹E方程；
（Ⅱ）过点B作直线交曲线E于点M、N，求△AMN面积的最小值．
查看习题详情和答案>>
| 2 |
（Ⅰ）建立适当坐标系，当O1位置变化时，求动点P的轨迹E方程；
（Ⅱ）过点B作直线交曲线E于点M、N，求△AMN面积的最小值．
如图，已知圆C:(x+1)2+y2=r2(r为常数，且r＞2)，定点B(1，0)，A是圆C上的动点，直线AC与线段AB的垂直平分线l相交于点M．当点A在圆C上移动一周时，点M的轨迹记为曲线F．
(1)求曲线F的方程；
(2)求证：直线l与曲线F只有一个公共点M；
(3)若r=4，点M在第一象限，且
，记直线l与直线CM的夹角为
，
求tan
．
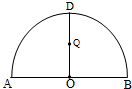如图所示，为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|+|PB|的值不变．
已知圆柱OO1底面半径为1，高为π，ABCD是圆柱的一个轴截面．动点M从点B出发沿着圆柱的侧面到达点D，其距离最短时在侧面留下的曲线Γ如图所示．将轴截面ABCD绕着轴OO1逆时针旋转θ（0＜θ＜π）后，边B1C1与曲线Γ相交于点P．