题目内容
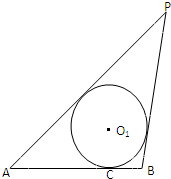 如图:已知线段AB=4,动圆O1与线段AB相切于点C,且AC-BC=2
如图:已知线段AB=4,动圆O1与线段AB相切于点C,且AC-BC=2| 2 |
(Ⅰ)建立适当坐标系,当O1位置变化时,求动点P的轨迹E方程;
(Ⅱ)过点B作直线交曲线E于点M、N,求△AMN面积的最小值.
分析:(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,可得|PA|-|PB|=|AC|-|BC|=2
,利用双曲线的定义,可得动点P的轨迹E方程;
(Ⅱ)设直线:x=my+2代入双曲线
-
=1,利用S△AMN=
×|AB|×|y1-y2|求出面积,换元,利用函数的单调性可得结论.
| 2 |
(Ⅱ)设直线:x=my+2代入双曲线
| x2 |
| 2 |
| y2 |
| 2 |
| 1 |
| 2 |
解答: 解:(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,则|PA|-|PB|=|AC|-|BC|=2
解:(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,则|PA|-|PB|=|AC|-|BC|=2
,
∴点P在以A、B为焦点双曲线上,且2c=4,2a=2
,
∴c=2,a=
,
∴b=
=
∴P点的轨迹E为:
-
=1(x>
);
(Ⅱ)设M(x1,y1),N(x2,y2),直线:x=my+2代入双曲线
-
=1得(m2-1)y2+4my+2=0,显然m≠±1
∵M、N在双曲线一支上,∴|m|<1.
S△AMN=
×|AB|×|y1-y2|=2
=2
令t=m2+1,有1≤t<2,则S△AMN=2
=2
在[1,2)上递增
∴当t=1,即m=0时,△AMN面积取得最小值为4
.
 解:(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,则|PA|-|PB|=|AC|-|BC|=2
解:(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,则|PA|-|PB|=|AC|-|BC|=2| 2 |
∴点P在以A、B为焦点双曲线上,且2c=4,2a=2
| 2 |
∴c=2,a=
| 2 |
∴b=
| c2-a2 |
| 2 |
∴P点的轨迹E为:
| x2 |
| 2 |
| y2 |
| 2 |
| 2 |
(Ⅱ)设M(x1,y1),N(x2,y2),直线:x=my+2代入双曲线
| x2 |
| 2 |
| y2 |
| 2 |
∵M、N在双曲线一支上,∴|m|<1.
S△AMN=
| 1 |
| 2 |
|
|
令t=m2+1,有1≤t<2,则S△AMN=2
|
|
∴当t=1,即m=0时,△AMN面积取得最小值为4
| 2 |
点评:本题考查双曲线定义的运用,考查直线与双曲线的位置关系,考查三角形面积的计算,考查函数的单调性,考查学生的计算能力,确定三角形的面积是关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,已知线段
如图,已知线段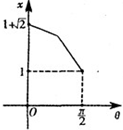
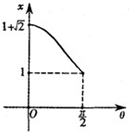
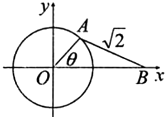
 (2012•自贡一模)如图,已知线段AB的长度为2,它的两个端点在⊙O的圆周上运动,则
(2012•自贡一模)如图,已知线段AB的长度为2,它的两个端点在⊙O的圆周上运动,则 内,线段
内,线段 ,
,  ,
,





