两列机械波相叠加出现稳定的干涉图样.由此可知( )A．两列机械波的频率不一定相等B．介质中振动加强的区域和振动减弱的区域总是互相间隔的C．振动加强的区域始终加强.振动减弱的区域始终减弱D．振动加强的区——青夏教育精英家教网——

两列机械波相叠加出现稳定的干涉图样，由此可知（）
A．两列机械波的频率不一定相等
B．介质中振动加强的区域和振动减弱的区域总是互相间隔的
C．振动加强的区域始终加强，振动减弱的区域始终减弱
D．振动加强的区域质点的位移总是比振动减弱的区域的质点的位移大

用绿光做双缝干涉实验，在光屏上呈现出明、暗相间的绿条纹，相邻两条绿条纹间的距离为△x．下列说法中正确的有（）
A．如果增大单缝到双缝间的距离，△x将增大
B．如果增大双缝之间的距离，△x将增大
C．如果增大双缝到光屏之间的距离，△x将增大
D．如果减小双缝的每条缝的宽度，而不改变双缝间的距离，△x将增大

如图所示是用频闪照相的方法拍下的一个弹簧振子的振动情况，甲图是振子静止在平衡位置时的照片，乙图是振子被拉伸到左侧距平衡位置20cm处，放手后，在向右运

周期内的频闪照片．丙图是振子从放手开始在

周期内的频闪照片．已知频闪的频率为9.0Hz，则相邻两次闪光的时间间隔t是 s，振动的周期T是 s，振子在1s内所走的路程是 m．

弦乐器小提琴是由两端固定的琴弦产生振动而发音的，如图甲所示，为了研究同一根琴弦振动频率与哪些因素有关，可利用图乙所示的实验装置，一块厚木板上有AB两个楔支撑着琴弦，其中A楔固定，B楔可沿木板移动来改变琴弦振动部分的长度，将琴弦的末端固定在木板O点，另一端通过滑轮接上砝码以提供一定拉力，轻轻拨动琴弦，在AB间产生振动．（不计摩擦）

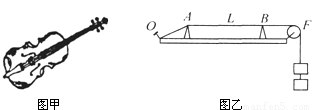
（1）先保持拉力为150N不变，改变AB的距离L（即改变琴弦长度），测出不同长度时琴弦振动的频率，记录结果如表1所示．
表1

长度大小L/m	1.00	0.85	0.70	0.55	0.40
振动频率f/Hz	150	176	214	273	375

从表1数据可判断在拉力不变时，琴弦振动的频率f与弦长L的关系为．
（2）保持琴弦长度为0.80m不变，改变拉力，测出不同拉力时琴弦振动的频率，记录结果如表2所示．
表2

拉力大小F/N	360	300	240	180	120
振动频率f/Hz	290	265	237	205	168

从表2数据可判断在琴弦长度不变时，琴弦振动的频率f与拉力F的关系为．
（3）综合上述两项测试可知当这根琴弦的长为0.75m，拉力为225N时，它的频率是 Hz（精确到个位数）．

单摆测定重力加速度的实验中

（1）实验时用20分度的游标卡尺测量摆球直径，示数如图甲所示，该摆球的直径d= mm．
（2）接着测量了摆线的长度为L，实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图乙所示，则重力加速度的表达式g= （用题目中物理量的字母表示）．
（3）某小组改变摆线长度L，测量了多组数据．在进行数据处理时，甲同学把摆线长L作为摆长，直接利用公式求出各组重力加速度值再求出平均值；乙同学作出T²-L图象后，如图丙所示，再利用图线上任意两点A、B的坐标（x₁，y₁）、（x₂，y₂），然后算出重力加速度g=4

两同学分别处理数据得到的结果和真实值相比较：甲，乙（填“偏大”、“偏小”或“无影响”）．

某同学在测定一厚度均匀的圆柱形玻璃砖的折射率时，先在白纸上作一与圆柱形玻璃同半径的圆，圆心为O，将圆柱形玻璃平放在白纸上，使其边界与所画的圆重合．在玻璃一侧竖直插两枚大头针P₁和P₂，在另一侧再先后插两枚大头针P₃和P₄，使从另一侧隔着玻璃观察时，大头针P₄、P₃和P₂、P₁的像恰在一条直线上．移去圆柱形玻璃和大头针后，得图：
①在图中画出光线在玻璃内外的传播方向；
②在光线的入射点做法线，并标出光由空气射入玻璃的入射角i和折射角r，写出计算玻璃折射率的公式n=______．
③若有一个折射率为

的透明玻璃球，让一束足够强的细光束在通过球心的平面内以45°入射角由空气射入玻璃球，则从各方向观察玻璃球，可以看到______束出射光线．

点光源S通过带有圆孔的遮光板N，照射到屏M上，形成直径为D的亮圆光斑，如果在N的前方、后方或M的前方分别放置足够大的平行玻璃砖（放置位置分别如图中1、2、3三个虚线框）时，屏M上的亮圆光斑直径分别为d₁、d₂、d₃，则：D和d₁、d₂、d₃的大小关系为：
D______d₁、D______d₂、D______d₃．

已知A、B是一列横波传播方向上平衡位置相距L的两点，当波传到A点时，A的起振方向是向上，且A起振后t秒时，B第一次下到波谷，而A则第三次到波峰，求该波的波长、周期及传播速度．

如图所示，在磁感应强度B=0.2T的水平匀强磁场中，有一边长为L=10cm，匝数N=100匝，总电阻r=1Ω的正方形线圈绕垂直于磁感线的OO′轴匀速转动，转速

r/s，有一电阻R=9Ω，通过电刷与两滑环接触，R两端接有一理想电压表，求：
（1）若从线圈通过中性面时开始计时，写出电动势的瞬时表达式．
（2）电压表的示数．
（3）在1分钟内外力驱动线圈转动所做的功．
（4）从图中所示位置转过90°的过程中通过电阻R的电量．

风能将成为21世纪大规模开发的一种可再生清洁能源．风力发电机是将风能（气流的功能）转化为电能的装置，其主要部件包括风轮机、齿轮箱，发电机等．如图所示．
（1）利用总电阻R=10Ω的线路向外输送风力发电机产生的电能．输送功率P=300 kW，输电电压U=10 kW，求异线上损失的功率与输送功率的比值；
（2）风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积．设空气密度为p，气流速度为v，风轮机叶片长度为r．求单位时间内流向风轮机的最大风能P_m；
在风速和叶片数确定的情况下，要提高风轮机单位时间接受的风能，简述可采取的措施．
（3）已知风力发电机的输出电功率P与P_m成正比．某风力发电机的风速v₁9m/s时能够输出电功率P₁=540kW．我国某地区风速不低于v₂=6m/s的时间每年约为5000小时，试估算这台风力发电机在该地区的最小年发电量是多少千瓦时．

0 66723 66731 66737 66741 66747 66749 66753 66759 66761 66767 66773 66777 66779 66783 66789 66791 66797 66801 66803 66807 66809 66813 66815 66817 66818 66819 66821 66822 66823 66825 66827 66831 66833 66837 66839 66843 66849 66851 66857 66861 66863 66867 66873 66879 66881 66887 66891 66893 66899 66903 66909 66917 176998