题目内容
单摆测定重力加速度的实验中
(1)实验时用20分度的游标卡尺测量摆球直径,示数如图甲所示,该摆球的直径d= mm.
(2)接着测量了摆线的长度为L,实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图乙所示,则重力加速度的表达式g= (用题目中物理量的字母表示).
(3)某小组改变摆线长度L,测量了多组数据.在进行数据处理时,甲同学把摆线长L作为摆长,直接利用公式求出各组重力加速度值再求出平均值;乙同学作出T2-L图象后,如图丙所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),然后算出重力加速度g=4
 两同学分别处理数据得到的结果和真实值相比较:甲 ,乙 (填“偏大”、“偏小”或“无影响”).
两同学分别处理数据得到的结果和真实值相比较:甲 ,乙 (填“偏大”、“偏小”或“无影响”).
【答案】分析:(1)由图示游标卡尺确定游标尺的精度,游标卡尺主尺示数与游标尺示数之和是游标卡尺的示数.
(2)单摆的摆长等于摆线的长度与摆球的半径之和,根据题意求出摆长.
摆球在最大位移处摆线的拉力最小,在最低点处,摆线的拉力最大,摆球从最大位移处,经最低点到达另一测最大位移处,然后再次反向通过最低点,最后回到最初的位置,经历的时间是一个周期,摆线的拉力经历三个最小值,由图乙所示图象求出单摆的周期T;最后由单摆周期公式求出重力加速度的表达式.
(3)根据单摆周期公式判断甲的测量值与真实值间的关系;由单摆周期公式的变形公式求出T2-L关系表达式,然后根据图丙所示图象求出重力加速度,然后判断测量值与真实值间的关系.
解答:解:(1)由图甲所示游标卡尺可知,游标尺是20分度的,游标尺的精度是0.05mm,
游标尺主尺示数是14mm,游标尺示数是3×0.05mm=0.15mm,
游标卡尺示数,即摆球的直径d=14mm+0.15mm=14.55mm.
(2)单摆摆长等于摆线长度与摆球半径之和,则单摆摆长为l=L+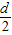 ,
,
由图乙所示图象可知,单摆的周期T=5t-t=4t,由单摆周期公式T=2π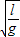 可知,
可知,
重力加速度g=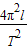 =
=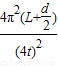 =
=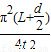 .
.
(3)由单摆周期公式T=2π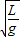 可知,重力加速度g=
可知,重力加速度g=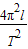 ,摆长应该是摆线长度与摆球半径之和,
,摆长应该是摆线长度与摆球半径之和,
甲同学把摆线长L作为摆长,摆长小于实际摆长,由g=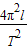 可知,重力加速度的测量值小于真实值;
可知,重力加速度的测量值小于真实值;
由T=2π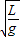 可知,L=
可知,L=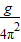 T2=kT2,其中k=
T2=kT2,其中k=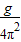 ,由此可见,L与T2成正比,k是比例常数;
,由此可见,L与T2成正比,k是比例常数;
由图丙可知,L与T2成正比,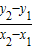 是图象的斜率k,所以k=
是图象的斜率k,所以k=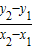 =
=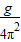 ,g=4π2
,g=4π2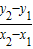 ,
,
由于单摆摆长偏大还是偏小不影响图象的斜率k=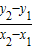 ,因此摆长偏小不影响重力加速度的测量值.
,因此摆长偏小不影响重力加速度的测量值.
故答案为:(1)14.15;(2)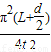 ;(3)偏小;无影响.
;(3)偏小;无影响.
点评:根据图乙所示图象求出单摆的周期是易错点,要掌握单摆的运动过程,结合图象求出单摆周期;熟练应用单摆周期公式是正确解题的关键.
(2)单摆的摆长等于摆线的长度与摆球的半径之和,根据题意求出摆长.
摆球在最大位移处摆线的拉力最小,在最低点处,摆线的拉力最大,摆球从最大位移处,经最低点到达另一测最大位移处,然后再次反向通过最低点,最后回到最初的位置,经历的时间是一个周期,摆线的拉力经历三个最小值,由图乙所示图象求出单摆的周期T;最后由单摆周期公式求出重力加速度的表达式.
(3)根据单摆周期公式判断甲的测量值与真实值间的关系;由单摆周期公式的变形公式求出T2-L关系表达式,然后根据图丙所示图象求出重力加速度,然后判断测量值与真实值间的关系.
解答:解:(1)由图甲所示游标卡尺可知,游标尺是20分度的,游标尺的精度是0.05mm,
游标尺主尺示数是14mm,游标尺示数是3×0.05mm=0.15mm,
游标卡尺示数,即摆球的直径d=14mm+0.15mm=14.55mm.
(2)单摆摆长等于摆线长度与摆球半径之和,则单摆摆长为l=L+
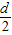 ,
,由图乙所示图象可知,单摆的周期T=5t-t=4t,由单摆周期公式T=2π
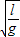 可知,
可知,重力加速度g=
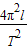 =
=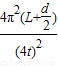 =
=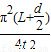 .
.(3)由单摆周期公式T=2π
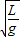 可知,重力加速度g=
可知,重力加速度g=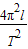 ,摆长应该是摆线长度与摆球半径之和,
,摆长应该是摆线长度与摆球半径之和,甲同学把摆线长L作为摆长,摆长小于实际摆长,由g=
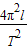 可知,重力加速度的测量值小于真实值;
可知,重力加速度的测量值小于真实值;由T=2π
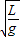 可知,L=
可知,L=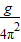 T2=kT2,其中k=
T2=kT2,其中k=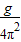 ,由此可见,L与T2成正比,k是比例常数;
,由此可见,L与T2成正比,k是比例常数;由图丙可知,L与T2成正比,
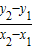 是图象的斜率k,所以k=
是图象的斜率k,所以k=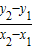 =
=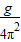 ,g=4π2
,g=4π2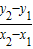 ,
,由于单摆摆长偏大还是偏小不影响图象的斜率k=
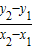 ,因此摆长偏小不影响重力加速度的测量值.
,因此摆长偏小不影响重力加速度的测量值.故答案为:(1)14.15;(2)
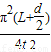 ;(3)偏小;无影响.
;(3)偏小;无影响.点评:根据图乙所示图象求出单摆的周期是易错点,要掌握单摆的运动过程,结合图象求出单摆周期;熟练应用单摆周期公式是正确解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目

 (2009?湘潭三模)在“用单摆测定重力加速度的实验中”
(2009?湘潭三模)在“用单摆测定重力加速度的实验中”