题目内容
8．如图所示，用水平力F把一铁块紧压在竖直墙壁上静止不动，当F增大时（ ）
| A． | 墙对铁块的弹力不变 | B． | 墙对铁块的弹力增大 | ||
| C． | 墙与铁块间的摩擦力减小 | D． | 墙对铁块的摩擦力不变 |
分析 当重力小于最大静摩擦力时，物体处于静止，摩擦力大小等于外力大小；当重力大于最大静摩擦力时，物体处于滑动，则摩擦力等于动摩擦力因数与正压力的乘积．
解答 解：用水平力F压铁块于竖直墙壁上不动，设墙壁对铁块的压力为N，对铁块的摩擦力为f，当F增大时，它的反作用力即墙壁对铁块的压力为N也增大．而铁块的摩擦力是由铁块的重力引起的，所以摩擦力不变．故AC错误，BD正确．
故选：BD
点评 学会区别静摩擦力与滑动摩擦力，且大小的计算．静摩擦力的大小等于引起它有运动趋势的外力，而滑动摩擦力等于μFN．同时知道作用力与反作用力跟平衡力的关系．
练习册系列答案
相关题目
粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时，在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A，如图，左、右管之间的距离忽略不计，左、右管长度都是6L，两水银柱的下表面到管口距离相等．大气压保持为p=4ρgL，ρ是水银的密度，g是重力加速度．把一侧的管口封住（不计厚度），再缓慢转动U形管，使其开口向上竖直放置，两侧水银柱的长度不变．
19．
如图所示，平行且足够长的两条光滑金属导轨，相距L=0.4m，导轨所在平面与水平面的夹角为30°，其电阻不计．把完全相同的两金属棒（长度均为0.4m）ab、cd分别垂直于导轨放置，并使每棒两端都与导轨良好接触．已知两金属棒的质量均为m=0.1kg、电阻均为R=0.2Ω，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B=0.5T，当金属棒ab在平行于导轨向上的力F作用下沿导轨向上匀速运动时，金属棒cd恰好能保持静止．（g=10m/s2），则（ ）
如图所示，平行且足够长的两条光滑金属导轨，相距L=0.4m，导轨所在平面与水平面的夹角为30°，其电阻不计．把完全相同的两金属棒（长度均为0.4m）ab、cd分别垂直于导轨放置，并使每棒两端都与导轨良好接触．已知两金属棒的质量均为m=0.1kg、电阻均为R=0.2Ω，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B=0.5T，当金属棒ab在平行于导轨向上的力F作用下沿导轨向上匀速运动时，金属棒cd恰好能保持静止．（g=10m/s2），则（ ）| A． | F的大小为0.5 N | |
| B． | 金属棒ab产生的感应电动势为1.0 V | |
| C． | ab两端的电压为1.0 V | |
| D． | ab棒的速度为5.0 m/s |
16．如图装置，不计滑轮的质量和绳与滑轮间的摩擦，整个装置处于平衡，则（ ）
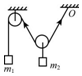
| A． | m1＞$\frac{1}{2}$m2 | |
| B． | m1＜$\frac{1}{2}$m2 | |
| C． | 若使m1的质量逐渐增加一些，整个装置一定能达到的平衡 | |
| D． | 若将右边绳子悬点O向右平移一些，则重物m2将会下降一些 |
13．辨别物质是晶体还是非晶体，比较正确的方法是（ ）
| A． | 从外形来判断 | B． | 从各向异性或各向同性来判断 | ||
| C． | 从导电性能来判断 | D． | 从是否具有确定的熔点来判断 |
如图所示，一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点，且两者固定不动．一长L为0.8m的细绳，一端固定于O点，另一端系一个质量m1为0.2kg的小球．当小球在竖直方向静止时，球对水平桌面的作用力刚好为零．现将球提起使细绳处于水平位置时无初速释放．当小球m1摆至最低点时，细绳恰好被拉断，此时小球m1恰好与放在桌面上的质量m2为0.8kg的小球正碰，碰后m1以2m/s的速度弹回，m2将沿半圆形轨道运动．两小球均可视为质点，取g=10m/s2．求：
18．某同学验证动能定理的实验装置如图甲所示．水平桌面上固定一倾斜的气垫导轨；导轨上A点处有一带遮光片的长方形滑块，其总质量为M，实验步骤如下：
①用游标卡尺测出遮光片的宽度d；
②安装好实验器材，给气垫导轨接上电源，然后读出拉力传感器的示数，记为F，同时从气垫导轨刻度尺上读出滑块与光电门之间的距离L；
③剪断细绳，让滑块滑向光电门，并记录滑块通过光电门的时间t；
④多次改变滑块与光电门之间的距离，记录相应的L与t的值，结果如表所示：
试分析下列问题：
（1）用游标卡尺测量遮光片宽度d的测量结果如图乙所示，则d=1.00cm．
（2）剪断细绳后，滑块开始加速下滑，则其受到的合外力为F．
（3）剪断细绳后，在滑块从A运动至B的过程中，合外力对滑块、遮光片组成的系统做的功可表示为W=FL，动能的增加量可表示为△Ek=$\frac{1}{2}$M（$\frac{d}{t}$）2；若动能定理成立，则在本实验中$\frac{1}{{t}^{2}}$与L的关系式为$\frac{1}{{t}^{2}}$=$\frac{2FL}{M{d}^{2}}$．
①用游标卡尺测出遮光片的宽度d；
②安装好实验器材，给气垫导轨接上电源，然后读出拉力传感器的示数，记为F，同时从气垫导轨刻度尺上读出滑块与光电门之间的距离L；
③剪断细绳，让滑块滑向光电门，并记录滑块通过光电门的时间t；
④多次改变滑块与光电门之间的距离，记录相应的L与t的值，结果如表所示：
| 1 | 2 | 3 | 4 | 5 | |
| L（m） | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| t（ms） | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| $\frac{1}{{t}^{2}}$（104s-2） | 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
（1）用游标卡尺测量遮光片宽度d的测量结果如图乙所示，则d=1.00cm．
（2）剪断细绳后，滑块开始加速下滑，则其受到的合外力为F．
（3）剪断细绳后，在滑块从A运动至B的过程中，合外力对滑块、遮光片组成的系统做的功可表示为W=FL，动能的增加量可表示为△Ek=$\frac{1}{2}$M（$\frac{d}{t}$）2；若动能定理成立，则在本实验中$\frac{1}{{t}^{2}}$与L的关系式为$\frac{1}{{t}^{2}}$=$\frac{2FL}{M{d}^{2}}$．