题目内容
1. 如图所示,在空间中存在垂直纸面向里的磁感应强度为B的匀强磁场,其边界AB、CD间的宽度为d,在左边界的Q点处有一质量为m,带电荷量为-q的粒子沿与左边界成30°的方向射入磁场,粒子重力不计.求:
如图所示,在空间中存在垂直纸面向里的磁感应强度为B的匀强磁场,其边界AB、CD间的宽度为d,在左边界的Q点处有一质量为m,带电荷量为-q的粒子沿与左边界成30°的方向射入磁场,粒子重力不计.求:(1)若带电粒子能从AB边界射出,则粒子入射速度应满足的条件;
(2)若带电粒子能垂直CD边界飞出磁场,进入如图所示的有界匀强电场中减速至零后再返回,则有界电场的电压的范围及整个过程中带电粒子在磁场中运动的时间;
(3)若带电粒子的速度是(2)中的$\sqrt{3}$倍,并可以从Q点沿纸面向各个方向射入磁场,则粒子打到CD边界上的长度是多少?
分析 (1)先作出粒子运动的轨迹,根据几何关系求出粒子能从左边界射出时临界情况的轨道半径,根据洛伦兹力提供向心力公式即可求解最大速度;
(2)根据几何知识求磁场中轨迹半径,由动能定理求极板间电压.
带电粒子能垂直CD边界飞出磁场,穿过小孔进入匀强电场中减速至零,然后由静止返回做匀加速运动,再进入磁场做匀速圆周运动,画出轨迹,确定磁场中运动轨迹对应的圆心角,求出通过磁场的时间.
(3)若带电粒子的速度是(2)中的$\sqrt{3}$倍,求出轨迹半径,画出轨迹,由几何知识求粒子能打到CD边界的范围.
解答 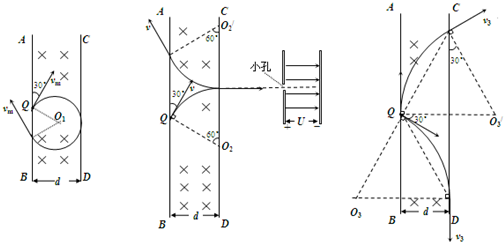 解:(1)粒子能从左边界射出,临界情况是轨迹与磁场右边界相切,粒子的运动轨迹如图所示,则有 R+Rcos30°=d
解:(1)粒子能从左边界射出,临界情况是轨迹与磁场右边界相切,粒子的运动轨迹如图所示,则有 R+Rcos30°=d
由$Bqv=m\frac{{v}^{2}}{R}$得 $v=\frac{Bqd}{m(1+cos30°)}$
所以粒子能从左边界射出速度应满足$v≤\frac{2(2-\sqrt{3})qBd}{m}$.
(2)粒子能从右边界垂直射出,由几何知识得R=$\frac{d}{cos30°}$
由$Bq{v}_{2}=m\frac{{{v}_{2}}^{2}}{R}$
在电场中:$\frac{1}{2}m{{v}_{2}}^{2}=Uq$
解得:
$U=\frac{{B}^{2}q{d}^{2}}{2m(cos30°)^{2}}=\frac{2{B}^{2}q{d}^{2}}{3m}$
故粒子不碰到右极板所加电压满足的条件$U≥\frac{2{B}^{2}q{d}^{2}}{3m}$
因粒子转过的圆心角为60°,所用时间为$\frac{T}{6}$,而$T=\frac{2πm}{Bq}$
因返回通过磁场所用时间相同,所以总时间 $t=2×\frac{T}{6}=\frac{2πm}{3Bq}$
(3)当粒子速度为是(2)中的$\sqrt{3}$倍时 解得 R′=2d粒子,如图
由几何关系可得l=2×2dcos30°=2$\sqrt{3}d$
答:(1)若带电粒子能从AB边界射出,则粒子入射速度应满足的条件为$v≤\frac{2(2-\sqrt{3})qBd}{m}$;
(2)有界电场的电压的范围为$U≥\frac{2{B}^{2}q{d}^{2}}{3m}$,整个过程中带电粒子在磁场中运动的时间为$\frac{2πm}{3qB}$;
(3)若带电粒子的速度是(2)中的$\sqrt{3}$倍,并可以从Q点沿纸面向各个方向射入磁场,则粒子打到CD边界上的长度是2$\sqrt{3}$d.
点评 带电粒子在磁场中的运动要把握其运动规律,在磁场中要注意找出相应的几何关系,从而确定圆心和半径,画出运动轨迹,难度适中.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
| A. | 环中感应电流的方向是顺时针方向 | |
| B. | 环中感应电流的大小不变 | |
| C. | 所施加水平拉力的大小要变 | |
| D. | 若将此环向左拉出磁场,则环中感应电流的方向也是顺时针方向 |
| A. | 加速过程中拉力做的功比匀速过程中拉力做的功多 | |
| B. | 匀速过程中拉力做的功比加速过程中拉力做的功多 | |
| C. | 两过程中拉力做的功一样多 | |
| D. | 无法比较 |
 如图所示,质量分别为m1=0.2kg、m2=0.3kg的A、B两等厚木板靠在一起静止于光滑水平面上,A的上表面光滑,B的上表面粗糙,一质量m=0.1kg的小物块以初速度v0=10m/s滑上A的表面,最后停在B上.求:
如图所示,质量分别为m1=0.2kg、m2=0.3kg的A、B两等厚木板靠在一起静止于光滑水平面上,A的上表面光滑,B的上表面粗糙,一质量m=0.1kg的小物块以初速度v0=10m/s滑上A的表面,最后停在B上.求: 如图所示,正方形匀强磁场磁感应强度B=0.2T,方向垂直于纸面向里,磁场的宽度为2L=2m,一正方形金属框边长L=1m,其单位长度电阻相等,总电阻为r=2Ω,金属框以v=10m/s的速度向右匀速穿过磁场区域.假定abcd方向的电流I为正,ab两端的电压为U,从cd边进入磁场瞬间开始计时,下列关于I-t和U-t图线正确的是( )
如图所示,正方形匀强磁场磁感应强度B=0.2T,方向垂直于纸面向里,磁场的宽度为2L=2m,一正方形金属框边长L=1m,其单位长度电阻相等,总电阻为r=2Ω,金属框以v=10m/s的速度向右匀速穿过磁场区域.假定abcd方向的电流I为正,ab两端的电压为U,从cd边进入磁场瞬间开始计时,下列关于I-t和U-t图线正确的是( )



