题目内容
5.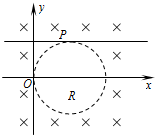 如图所示,在xOy竖直平面内有一半径为R与y轴相切于O点的圆,圆上一点P的坐标为(R,R),平行于x轴的直线与圆相切于P点.除该圆形区域外,xOy平面内均存在相互垂直的匀强磁场和匀强电场,磁感应强度大小为B,方向垂直纸面向里.现从P点向y≥R一侧沿xOy的各个不同方向发射带正电的微粒,微粒的质量为m,电荷量为q,速度大小相同,在电场和磁场区域做匀速圆周运动,均能平行于沿x轴的正方向进入圆形区域.重力加速度为g,圆形区域的边界在电场磁场中.
如图所示,在xOy竖直平面内有一半径为R与y轴相切于O点的圆,圆上一点P的坐标为(R,R),平行于x轴的直线与圆相切于P点.除该圆形区域外,xOy平面内均存在相互垂直的匀强磁场和匀强电场,磁感应强度大小为B,方向垂直纸面向里.现从P点向y≥R一侧沿xOy的各个不同方向发射带正电的微粒,微粒的质量为m,电荷量为q,速度大小相同,在电场和磁场区域做匀速圆周运动,均能平行于沿x轴的正方向进入圆形区域.重力加速度为g,圆形区域的边界在电场磁场中.(1)求匀强电场的电场强度;
(2)求带电微粒在磁场中运动的速度;
(3)若某微粒从O点进入圆形区域,从M点(图中未标出)离开圆形区域,OM与x轴成θ角,求该微粒从P点到M点运动的时间.
分析 (1)微粒在电磁场中做匀速圆周运动,电场力与重力合力为零,据此求出电场强度.
(2)由几何知识求出微粒做匀速圆周运动的轨道半径,然后由牛顿第二定律求出微粒的速度.
(3)求出微粒在磁场中做圆周运动的时间,求出微粒在圆形区域的运动时间,然后求出微粒总的运动时间.
解答 解:(1)带电粒子在电磁场中做匀速圆周运动,则电场力与重力合力为零,
微粒在竖直方向处于平衡状态:qE=mg,解得:E=$\frac{mg}{q}$;
(2)选取任意带电微粒做圆周运动,设半径为r,平行x轴正方向进入圆形区域,如图所示.
由几何关系可得:SP、NQ均垂直于x轴,且NQ、NP和SQ、SP分别为两圆的半径,
因此:△NPS≌△NQS,故四边形SPNQ为菱形,可得:r=R,
带电微粒在磁场中做匀速圆周运动,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{qBR}{m}$;
(3)微粒电磁场中做匀速圆周运动,设微粒做圆周运动时间为t1,
由于微粒沿x轴进入圆形区域,故两圆心与两圆交点的连线组成正方形,
圆周运动对应的圆心角:θ=$\frac{3π}{2}$. 
微粒在磁场中的运动时间:t1=$\frac{θ}{2π}$T=$\frac{θ}{2π}$×$\frac{2πm}{qB}$=$\frac{θm}{qB}$=$\frac{3πm}{2qB}$,
微粒在圆形区域内在重力作用下平抛运动,设运动时间为t2,
OM与x轴成θ角,设速度方向与x轴方向夹角为α,
由平抛运动规律可知:tanα=2tanθ,tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{g{t}_{2}}{{v}_{0}}$,解得:t2=$\frac{2qBRtanθ}{mg}$,
微粒从O点进入圆形区域,从M点离开圆形区域所用的总时间为:t=t1+t2=$\frac{3πm}{2qB}$+$\frac{2qBRtanθ}{mg}$;
答:(1)匀强电场的电场强度$\frac{mg}{q}$;
(2)带电微粒在磁场中运动的速度为$\frac{qBR}{m}$;
(3)该微粒从P点到M点运动的时间为$\frac{3πm}{2qB}$+$\frac{2qBRtanθ}{mg}$.
点评 带电粒子在复合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况,再选择合适方法处理.对于匀变速曲线运动,常常运用运动的分解法,将其分解为两个直线的合成,由牛顿第二定律和运动学公式结合求解;对于磁场中圆周运动,要正确画出轨迹,由几何知识求解半径.

| A. | 平抛运动是匀变速运动 | |
| B. | 平抛运动的水平位移只与水平速度有关 | |
| C. | 平抛运动的速度和加速度方向不断变化 | |
| D. | 平抛运动的飞行时间只取决于初始位置的高度 |
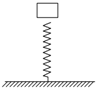 如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )| A. | 物体和弹簧接触时,物体的动能最大 | |
| B. | 物体在反弹阶段,动能一直增加,直到物体脱离弹簧为止 | |
| C. | 与弹簧接触的整个过程,物体的动能与重力势能之和先增大后减小 | |
| D. | 与弹簧接触的整个过程,物体的动能与弹簧弹性势能之和先增大后减小 |
 如图1所示,放在斜面上的物体静止,若加入一个垂直斜面的外力F作用物体上,物体仍静止(如图2).动摩擦因数μ,物体质量m,斜面倾角θ,则( )
如图1所示,放在斜面上的物体静止,若加入一个垂直斜面的外力F作用物体上,物体仍静止(如图2).动摩擦因数μ,物体质量m,斜面倾角θ,则( )| A. | 物体受到的摩擦力一定是μmgcosθ | |
| B. | 一定有μ≥tanθ | |
| C. | 物体可能受三个力作用,也可能受四个力作用 | |
| D. | 物体一定受四个力作用 |
 如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )
如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )| A. | 地面对B的支持力大于(M+m)g | |
| B. | A对B的压力的最小值为$\frac{\sqrt{3}mg}{2}$,最大值为$\frac{3\sqrt{3}mg}{4}$ | |
| C. | A受到摩擦力的最小值为0,最大值为$\frac{mg}{4}$ | |
| D. | A受到摩擦力的最小值为$\frac{mg}{2}$,最大值为$\frac{3mg}{4}$ |
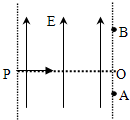 如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )
如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )| A. | 两个粒子电性相反 | |
| B. | 两个粒子在电场中运动的时间不一样 | |
| C. | 两个粒子做匀速圆周运动 | |
| D. | 两个粒子的电势能均减小 |
 如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度.
如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度. 如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求:
如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求: