题目内容
19.静止状态的原子核X,放出一个α粒子后变成质量为M的新原子核(无光子放出).被放出的α粒子垂直进入磁感应强度为B的匀强磁场,测得其圆周运动的半径为r.设α粒子质量为m,质子带电量为e,则( )| A. | α粒子的速率为$\frac{2eBr}{m}$ | |
| B. | 新原子核的速率为$\frac{2eBr}{M}$ | |
| C. | 该反应质量亏损为$△m=\frac{{4{e^2}{B^2}{r^2}(M+m)}}{{Mm{c^2}}}$ | |
| D. | 原子核X的质量为$M+m+\frac{{2{e^2}{B^2}{r^2}(M+m)}}{{Mm{c^2}}}$ |
分析 根据洛伦兹力提供向心力求出α粒子的速率,结合动量守恒定律求出新原子核的速率.根据释放的能量求出质量亏损,从而得出原子核X的质量.
解答 解:A、根据$qvB=m\frac{{v}^{2}}{r}$得,α粒子的速率$v=\frac{qBr}{m}=\frac{2eBr}{m}$,故A正确.
B、根据动量守恒定律得,0=Mv′-mv,解得新原子核的速率$v′=\frac{mv}{M}=\frac{2eBr}{M}$,故B正确.
C、释放的能量全部转化为α粒子和新核的动能,即$△E=\frac{1}{2}m{v}^{2}+\frac{1}{2}Mv{′}^{2}$=$\frac{2{e}^{2}{B}^{2}{r}^{2}(M+m)}{Mm}$,则质量亏损△m=$\frac{2{e}^{2}{B}^{2}{r}^{2}(M+m)}{Mm{c}^{2}}$,所以原子核X的质量为$M+m+\frac{{2{e^2}{B^2}{r^2}(M+m)}}{{Mm{c^2}}}$,故C错误,D正确.
故选:ABD.
点评 本题考查了动量守恒和衰变的综合运用,掌握粒子在磁场中的半径公式和爱因斯坦质能方程是解决本题的关键.

练习册系列答案
相关题目
2.对于利用自由落体“验证机械能守恒定律”的实验中,下列说法正确的是.( )
| A. | 本实验应选择体积较小、质量较大的重物,以便减小误差 | |
| B. | 本实验可以不测量重物的质量 | |
| C. | 必须先松开纸带后接通电源,以便减小误差 | |
| D. | 物体由静止开始自由下落到某点时的瞬时速度v,可以通过v=$\sqrt{2gh}$计算 |
3.下列说法正确的是( )
| A. | 动量的方向与所受合外力方向一定相同 | |
| B. | 动量的方向与合外力冲量的方向一定相同 | |
| C. | 动量增加的方向与合外力方向一定相同 | |
| D. | 动量变化率的方向与速度方向一定相同 |
7.质量为m的物体在水平面上,只受摩擦力作用,以初动能E0做匀变速直线运动,经距离d后,动能减为$\frac{{E}_{0}}{3}$,则( )
| A. | 物体与水平面间的动摩擦因数为$\frac{2{E}_{0}}{3mgd}$ | |
| B. | 物体再前进$\frac{d}{3}$便停止 | |
| C. | 物体滑行距离d所用时间是滑行后面距离所用时间的$\sqrt{3}$倍 | |
| D. | 若要使此物体滑行的总距离为3d,其初动能应为2E0 |
14. 有一条长为2m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为( )(g取10m/s2)
有一条长为2m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为( )(g取10m/s2)
 有一条长为2m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为( )(g取10m/s2)
有一条长为2m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为( )(g取10m/s2)| A. | 2.5m/s | B. | 2.5$\sqrt{2}$m/s | C. | $\sqrt{5}$m/s | D. | 0.5$\sqrt{35}$m/s |
4.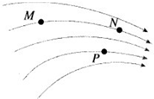 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点.下列判断正确的是( )| A. | M、N、P三点中M点的场强最大 | |
| B. | M、N、P三点中N点的电势最高 | |
| C. | 负电荷在M点的电势能小于在N点的电势能 | |
| D. | 正电荷从M点自由释放,电荷将沿电场线运动到N点 |
11. 足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
 足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )
足球比赛中踢点球时,足球距球门14.00m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知球门高度约2.45m,足球质量约400g,不计空气阻力,则该球员此次踢球过程中对足球做的功约为(g取10m/s2)( )| A. | 30 J | B. | 60 J | C. | 90 J | D. | 120 J |
8. 如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
 如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )
如图所示,质量为m的物块放在地面上,在力F的作用下保持静止.经过时间t,重力的冲量是( )| A. | mgt | B. | Ft | C. | (mg+F)t | D. | 0 |
4.关于近代物理,下列说法正确的是( )
| A. | 用光照射金属不能发生光电效应是因为该入射光的频率小于金属的截止频率 | |
| B. | 核聚变反应方程${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n中,${\;}_{0}^{1}$n表示质子 | |
| C. | α射线是高速运动的氦原子 | |
| D. | 由玻尔的原子模型可推知,处于激发态的氢原子,量子数越大,核外电子动能越小 |