��Ŀ����
14����ͼ����ʾ���⻬��ƽ�н�������ˮƽ���ã�������Ϊl������һ��ֵΪR�ĵ��裮��MN��PQ֮����ڴ�ֱ���ƽ����н���ǿ�ų����ų�����Ϊd��һ����Ϊm�Ľ�����ab���ڵ����ϣ��뵼�촹ֱ�ҽӴ����ã����Ƶ���ͽ������ĵ��裮������ab��ˮƽ��F=$\sqrt{0.2x}$+0.4��N�������ã�����xΪ��������MN�ľ��룬F��x�Ĺ�ϵ��ͼ����ʾ��������ab�Ӵų�����߽��ɾ�ֹ��ʼ�˶���ͨ����ѹ��������õ���R���˵�ѹ��ʱ�����������֪l=1m��m=1kg��R=0.5����d=1m���ʣ���1���������տ�ʼ�˶�ʱ�ļ��ٶ�Ϊ���٣����жϸý������ڴų����������˶���
��2���Ÿ�Ӧǿ��B�Ĵ�СΪ���٣�
��3����ijʱ�̳�ȥ����F������ٶ�v��λ��s�ı仯��������v=v0-$\frac{{{B^2}{l^2}}}{mR}$s��v0Ϊ��ȥ����ʱ���ٶȣ�sΪ��ȥ����F���λ�ƣ����Ұ��˶���PQ��ʱǡ�þ�ֹ��������F���õ�ʱ��Ϊ���٣�
��4���ڣ�3��������£���������MN�˶���PQ������������������R����������ԼΪ���٣�

���� ��1���Խ���������������Ȼ����ţ�ٵڶ�����������ٶȣ��������⣬Ӧ��E=BLv�жϽ��������˶����ʣ�
��2����ͼ�����x��F�Ķ�Ӧֵ��Ӧ��ţ�ٵڶ���������Ÿ�Ӧǿ�ȣ�
��3�����ȱ���ֱ���˶���λ�ƹ�ʽ��������������λ�ƣ�Ȼ�������������ʱ�䣻
��4���˷�����������ת��Ϊ�����ȣ��ɶ��ܶ����������R������������
��� �⣺��1���������տ�ʼ�˶�ʱx=0����v=0�����ܰ��������ã����Դ�ʱ���ܺ�����Ϊ��
F=$\sqrt{0.2x}+0.4$=0.4N��
��ţ�ٵڶ����ɵã�a=$\frac{F}{m}=\frac{0.4}{1}$m/s2=0.4m/s2
�����⣬����R���˵�ѹ��ʱ����������������и�Ÿ��߲����ĵ綯����ʱ����������ݦ�=Blv����֪���������ٶ���ʱ������������Խ����������ٶ�Ϊ����ȼ����˶�
��2�������������ٶ�Ϊ�㣬���ٶ�Ϊa=0.4m/s2���ȱ����˶�����$v=\sqrt{2ax}$����
��ţ�ٵڶ�����֪��$F-\frac{{{B^2}{l^2}v}}{R}=ma$����
��F=$\sqrt{0.2x}+0.4$��
����ã�$��\sqrt{0.2}-\frac{{{B^2}{l^2}}}{R}\sqrt{2a}��\sqrt{x}+0.4=ma$
���� $\sqrt{0.2}-\frac{{{B^2}{l^2}}}{R}\sqrt{2a}=0$����
��ã�$B=\sqrt{\frac{{\sqrt{0.2}R}}{{\sqrt{2a}{l^2}}}}=\sqrt{\frac{{\sqrt{0.2}•0.5}}{{\sqrt{2•0.4}��{1^2}}}}T=0.5T$����
��ͼ�ҿ�֪����x=0.8mʱ��F=0.8N�������ʽ��$0.8-\frac{{{B^2}��{1^2}}}{0.5}\sqrt{2��0.4��0.8}=1��0.4$����
��ã�B=0.5T����
��3��������F���õ�ʱ��Ϊt������F����ʱ�������˶����룺$x=\frac{1}{2}a{t^2}$��
��ȥ��������������ٶ�Ϊ��$v={v_0}-\frac{{{B^2}{l^2}}}{mR}s$��
��PQǡ�þ�ֹ������v=0��v0=at��
�ó�ȥ������������˶����룺$s=\frac{mR}{{{B^2}{l^2}}}•at$��
���$\frac{1}{2}a{t^2}+\frac{mR}{{{B^2}{l^2}}}•at=d$
���������ֵ���ã�0.2t2+0.8t-1=0��
��ã�t=1s
��4����F����ʱ�������˶����룺$x=\frac{1}{2}a{t^2}=\frac{1}{2}��0.4��{1^2}m=0.2m$
��F-xͼ��֪ͼ����ᡢ����������Χ��������ڴ˹���������F���Ĺ�WF��ͨ�������ӿ�֪WFԼΪ0.11J��
��������MN��ʼ�˶���PQ�߾�ֹ���ɶ��ܶ����ã�WF+W��=0
���Ե���R����������Ϊ��QR=-W��=WF=0.11J
�𣺣�1���������տ�ʼ�˶�ʱ�ļ��ٶ�Ϊ0.44m/s2���ý������ڴų��г��ٶ�Ϊ����ȼ����˶�
��2���Ÿ�Ӧǿ��B�Ĵ�СΪ0.5T��
��3������F���õ�ʱ��Ϊ1s��
��4���ڣ�3��������£���������MN�˶���PQ������������������R����������ԼΪ0.11J��
���� ������һ����Ÿ�Ӧ����ѧ���ϵ��ۺ��⣬�ѶȽϴ���������������˶����̡�Ӧ����Ŀ����������ţ�ٵڶ����ɡ��˶�ѧ��ʽ������ȷ���⣻����R�������������ڿ˷������������Ĺ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ���û���ЧӦ�����Ļ���Ԫ�����㷺Ӧ���ڲ������Զ����Ƶ�������ͼ�ǻ���Ԫ���Ĺ���ԭ��ʾ��ͼ���Ÿ���ǿ��B��ֱ�ڻ���Ԫ���Ĺ��������£�E��FΪǰ����棬ͨ��ͼʾ����ĵ���I��C��D��������γɵ��Ʋ�UCD������˵������ȷ���ǣ�������
���û���ЧӦ�����Ļ���Ԫ�����㷺Ӧ���ڲ������Զ����Ƶ�������ͼ�ǻ���Ԫ���Ĺ���ԭ��ʾ��ͼ���Ÿ���ǿ��B��ֱ�ڻ���Ԫ���Ĺ��������£�E��FΪǰ����棬ͨ��ͼʾ����ĵ���I��C��D��������γɵ��Ʋ�UCD������˵������ȷ���ǣ�������| A�� | ���Ʋ�UCD��������й� | |
| B�� | ������Ԫ���������������ɵ��ӣ�����Ʋ�UCDΪ�� | |
| C�� | ������Ÿ�Ӧǿ��ʱ�����Ʋ�UCD��� | |
| D�� | �ڲ����������Ϸ��ĵشų�ǿ��ʱ��Ԫ���Ĺ�����Ӧ����ˮƽ����ͼ����ʾ�� |
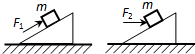 ��ͼ��ʾ���ֱ�����������F1��F2���Ⱥ����ν�����Ϊm������Ӿ�ֹ��ʼ����ͬһ���ֲڵĹ̶�б���ɵ��Ƶ����ˣ���һ����F1�ķ�����б�����ϣ��ڶ�����F2�ķ�����ˮƽ���ң��������õ�ʱ����ͬ���������������У�������
��ͼ��ʾ���ֱ�����������F1��F2���Ⱥ����ν�����Ϊm������Ӿ�ֹ��ʼ����ͬһ���ֲڵĹ̶�б���ɵ��Ƶ����ˣ���һ����F1�ķ�����б�����ϣ��ڶ�����F2�ķ�����ˮƽ���ң��������õ�ʱ����ͬ���������������У�������| A�� | F1��F2��������ƽ������һ����ͬ | B�� | �����е�ܱ仯һ����ͬ | ||
| C�� | F1��F2������ij�����Сһ����ͬ | D�� | ����˷�Ħ�������Ĺ�һ����ͬ |
| A�� | v��7.9 km/s | B�� | v=7.9km/s | ||
| C�� | 11.2km/s��v��7.9km/s | D�� | v��11.2km/s |
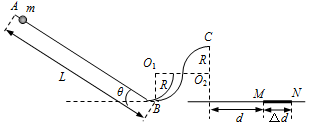
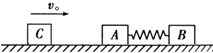 ��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ���ABC�����壬A��B��һ�������õ����ʵ�������һ�𣬿�ʼ���ɴ���ԭ����A��B����ֹ��A��B��������ΪM=2kg����һ����C�Գ��ٶ�v0=6m/sˮƽ�����˶���C��A��ײ��ճ����һ������ײʱ�伫�̣���֪C������Ϊm=1kg����
��ͼ��ʾ���ڹ⻬ˮƽ���Ϸ���ABC�����壬A��B��һ�������õ����ʵ�������һ�𣬿�ʼ���ɴ���ԭ����A��B����ֹ��A��B��������ΪM=2kg����һ����C�Գ��ٶ�v0=6m/sˮƽ�����˶���C��A��ײ��ճ����һ������ײʱ�伫�̣���֪C������Ϊm=1kg����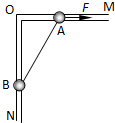 ��ͼ��ʾ����ֱƽ���ڷ�һֱ�Ǹ�MON��OMˮƽ��ON��ֱ�ҹ⻬���ò����쳤��������������С��A��B�ֱ�����OM��ON���ϣ�B�������Ϊ2kg����������A���ˮƽ��F�������£�A��B�����ھ�ֹ״̬����ʱOA=0.3m��OB=0.4m���ı�ˮƽ��F�Ĵ�С��ʹA�����Ҽ����˶�����֪A�������˶�0.1mʱ�ٶȴ�СΪ3m/s�����ڴ˹���������B������������Ĺ�Ϊ��ȡg=10m/s2����������
��ͼ��ʾ����ֱƽ���ڷ�һֱ�Ǹ�MON��OMˮƽ��ON��ֱ�ҹ⻬���ò����쳤��������������С��A��B�ֱ�����OM��ON���ϣ�B�������Ϊ2kg����������A���ˮƽ��F�������£�A��B�����ھ�ֹ״̬����ʱOA=0.3m��OB=0.4m���ı�ˮƽ��F�Ĵ�С��ʹA�����Ҽ����˶�����֪A�������˶�0.1mʱ�ٶȴ�СΪ3m/s�����ڴ˹���������B������������Ĺ�Ϊ��ȡg=10m/s2����������