题目内容
10.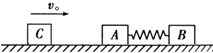 如图所示,在光滑水平面上放置ABC三物体,A与B用一弹性良好的轻质弹簧连在一起,开始弹簧处于原长,A、B均静止.A、B的质量均为M=2kg,另一物体C以初速度v0=6m/s水平向右运动,C与A碰撞后粘合在一起,设碰撞时间极短,已知C的质量为m=1kg.求:
如图所示,在光滑水平面上放置ABC三物体,A与B用一弹性良好的轻质弹簧连在一起,开始弹簧处于原长,A、B均静止.A、B的质量均为M=2kg,另一物体C以初速度v0=6m/s水平向右运动,C与A碰撞后粘合在一起,设碰撞时间极短,已知C的质量为m=1kg.求:(1)弹簧弹性势能的最大值
(2)在以后的运动过程中物体B的最大速度.
分析 (1)根据定律守恒求出AC的共同速度,当A、B、C三者的速度相等时弹簧的弹性势能最大,根据动量守恒及能量守恒求出弹性势能的最大值;
(2)当弹簧第一次恢复原长时,B的速度最大,设此时B的速度为vB,从A、C粘合到弹簧第一次恢复原长的过程中,根据动量守恒及能量守恒求出最大速度.
解答 解:(1)C与A碰撞过程,设共同速度v1,以向右为正,由动量守恒:
mv0=(m+M)v1
代入数据解得:v1=2m/s
当A、B、C速度相等时,弹簧被压缩到最短,弹簧的弹性势能最大,设此时三物体速度为v共,有:
(m+M)v1=(m+2M)v共
代入数据解得:v共=1.2m/s
根据能量守恒得:${E_{pmax}}=\frac{1}{2}(m+M)v_1^2-\frac{1}{2}(m+2M)v_共^2$
代入数据解得:Epmax=2.4J
(2)当弹簧第一次恢复原长时,B的速度最大,设此时B的速度为vB,从A、C粘合到弹簧第一次恢复原长的过程,设此时A、C的速度为v1′,
由动量守恒和能量守恒有:
(m+M)v1=(m+M)v1′+MvB,
$\frac{1}{2}(m+M)v_1^2=\frac{1}{2}(m+M){v_1}{'^2}+\frac{1}{2}Mv_B^2$
${v_B}=\frac{2(m+M)}{m+2M}{v_1}$
解得:vB=2.4m/s,故B的速度最大为2.4m/s,方向向右.
答:(1)弹簧弹性势能的最大值为2.4J;
(2)在以后的运动过程中物体B的最大速度大小为2.4m/s,方向向右.
点评 本题考查了动量守恒和能量守恒定律的综合运用,知道三者速度相等时,弹性势能最大,明确应用动量守恒定律解题时,要规定正方向,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理如图所示,利用与飞机前轮连接的通电导体在两平行金属导轨的强电流产生的磁场中受安培力作用下匀加速获得动能.设飞机质量为m=1.8×104kg,起飞速度为v=70m/s,起飞过程所受平均阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始起飞距离为L=210m;在电磁弹射器与飞机发动机(牵引力不变)同时工作的情况下,起飞距离减为L/3.取g=10m/s2,以下说法正确的是( )
我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理如图所示,利用与飞机前轮连接的通电导体在两平行金属导轨的强电流产生的磁场中受安培力作用下匀加速获得动能.设飞机质量为m=1.8×104kg,起飞速度为v=70m/s,起飞过程所受平均阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始起飞距离为L=210m;在电磁弹射器与飞机发动机(牵引力不变)同时工作的情况下,起飞距离减为L/3.取g=10m/s2,以下说法正确的是( )
 我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理如图所示,利用与飞机前轮连接的通电导体在两平行金属导轨的强电流产生的磁场中受安培力作用下匀加速获得动能.设飞机质量为m=1.8×104kg,起飞速度为v=70m/s,起飞过程所受平均阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始起飞距离为L=210m;在电磁弹射器与飞机发动机(牵引力不变)同时工作的情况下,起飞距离减为L/3.取g=10m/s2,以下说法正确的是( )
我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理如图所示,利用与飞机前轮连接的通电导体在两平行金属导轨的强电流产生的磁场中受安培力作用下匀加速获得动能.设飞机质量为m=1.8×104kg,起飞速度为v=70m/s,起飞过程所受平均阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始起飞距离为L=210m;在电磁弹射器与飞机发动机(牵引力不变)同时工作的情况下,起飞距离减为L/3.取g=10m/s2,以下说法正确的是( )| A. | 在没有电磁弹射器的情况下.飞机所受牵引力F=2.1×105N | |
| B. | 在没有电磁弹射器的情况下,飞机所受牵引力F=2.46×105N | |
| C. | 在电磁弹射器与飞机发动机同时工作时,若只增大电流,则起飞的距离将更小 | |
| D. | 在电磁弹射器与飞机发动机同时工作时,电磁弹射器对飞机做的功W=2.94×107J |
1. 如图所示,在两等量异种点电荷连线上有D、E、F三点,且DE=EF.K、M、L分别为过D、E、F三点的等势面.一不计重力的带负电粒子,从a点射入电场,运动轨迹如图中实线所示,以|Wab|表示该粒子从a点到b点电场力做功的数值,以|Wbc|表示该粒子从b点到c点电场力做功的数值,则( )
如图所示,在两等量异种点电荷连线上有D、E、F三点,且DE=EF.K、M、L分别为过D、E、F三点的等势面.一不计重力的带负电粒子,从a点射入电场,运动轨迹如图中实线所示,以|Wab|表示该粒子从a点到b点电场力做功的数值,以|Wbc|表示该粒子从b点到c点电场力做功的数值,则( )
 如图所示,在两等量异种点电荷连线上有D、E、F三点,且DE=EF.K、M、L分别为过D、E、F三点的等势面.一不计重力的带负电粒子,从a点射入电场,运动轨迹如图中实线所示,以|Wab|表示该粒子从a点到b点电场力做功的数值,以|Wbc|表示该粒子从b点到c点电场力做功的数值,则( )
如图所示,在两等量异种点电荷连线上有D、E、F三点,且DE=EF.K、M、L分别为过D、E、F三点的等势面.一不计重力的带负电粒子,从a点射入电场,运动轨迹如图中实线所示,以|Wab|表示该粒子从a点到b点电场力做功的数值,以|Wbc|表示该粒子从b点到c点电场力做功的数值,则( )| A. | |Wab|>|Wbc| | B. | |Wab|=|Wbc| | ||
| C. | 粒子由a点到b点,动能减少 | D. | a点的电势较b点的电势低 |
18. 一人乘电梯上楼,在竖直上升过程中加速度a 随时间t 变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
一人乘电梯上楼,在竖直上升过程中加速度a 随时间t 变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
 一人乘电梯上楼,在竖直上升过程中加速度a 随时间t 变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
一人乘电梯上楼,在竖直上升过程中加速度a 随时间t 变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )| A. | t=2 s 时最小 | B. | t=2 s 时最大 | C. | t=8.5 s 时最小 | D. | t=8.5 s 时最大 |
5. 如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为$\frac{5g}{8}$,这物体在斜面上上升的最大高度为h,则物体在斜面上运动的整个过程中( )
如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为$\frac{5g}{8}$,这物体在斜面上上升的最大高度为h,则物体在斜面上运动的整个过程中( )
 如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为$\frac{5g}{8}$,这物体在斜面上上升的最大高度为h,则物体在斜面上运动的整个过程中( )
如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为$\frac{5g}{8}$,这物体在斜面上上升的最大高度为h,则物体在斜面上运动的整个过程中( )| A. | 上升过程物体动能减少了$\frac{5}{4}$mgh | |
| B. | 上升过程重力势能增加了$\frac{5}{8}$mgh | |
| C. | 物体在斜面上运动的整个过程机械能损失了$\frac{1}{2}$mgh | |
| D. | 物体沿斜面上升过程克服重力做功的平均功率小于下降过程重力做功的平均功率 |
15.下列有关光的现象、电磁波和相对论的说法正确的是( )
| A. | 光通过偏振片时,光的振动方向与透振方向的夹角越大,透过的光越强 | |
| B. | 杨氏干涉观察到了明暗条纹证明光是一种波,如果用激光进行实验则效果没有那么明显 | |
| C. | 赫兹在实验中发现,当电磁波到达导线环时,它在导线环中激发出感应电动势,使得导线环中产生火花,这个导线环就是一个电磁波检测器 | |
| D. | 根据相对论原理,将两只调整同步的铯原子钟分别放在地面上和宇宙飞船上,则在宇宙飞船上的铯原子钟会走得慢些 |
2.下列属于国际单位制中基本单位的一组是( )
| A. | 米、千克、秒 | B. | 长度、质量、时间 | C. | 位移、速度、力 | D. | 米、米/秒、牛顿 |
19. 如图所示,两根相互平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、O、b在M、N的连线上,O为MN的中点.c、d位于MN的中垂线上,且a、b、c、d到O点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )
如图所示,两根相互平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、O、b在M、N的连线上,O为MN的中点.c、d位于MN的中垂线上,且a、b、c、d到O点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )
 如图所示,两根相互平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、O、b在M、N的连线上,O为MN的中点.c、d位于MN的中垂线上,且a、b、c、d到O点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )
如图所示,两根相互平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、O、b在M、N的连线上,O为MN的中点.c、d位于MN的中垂线上,且a、b、c、d到O点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )| A. | O点处的磁感应强度为零 | |
| B. | a、b两点处的磁感应强度大小相等,方向相同 | |
| C. | c、d两点处的磁感应强度大小相等,方向相同 | |
| D. | a、c两点处的磁感应强度的方向相同 |
