题目内容
6.某种娱乐比赛的示意图如图所示,质量为m=0.1kg的小球穿在长为L的杆上(L足够长),它们间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,两个半径都为R=0.4m的四分之一圆轨道拼接后与杆在B点平滑连接(连接处长度不计),两个圆的圆心O1、Q2等高,圆轨道可视为光滑,C点切线水平,整个装置处于同一竖直平面内,离C点水平距离为d=0.8m的得分区MN,其宽度为△d=$\frac{d}{2}$,若每次小球都从杆上由静止释放,杆与水平面的夹角θ可调,重力加速度g取10m/s2,请回答: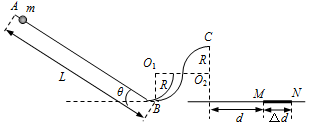
(1)小球离开C点时的速度多大才能落在得分区的M点?
(2)落在M点的小球在C处时,轨道对小球的作用力多大?
(3)若θ=60°,小球在杆上离B点多少距离处释放才能落在得分区?
分析 (1)小球离开C点时做平抛运动,已知平抛运动的水平位移和竖直位移,由分位移公式可求得C点的速度.
(2)在C点,由合力提供向心力,由牛顿第二定律求解.
(3)先由平抛运动的规律得到小球要落在N点,经过C点的速度,从而得到落在得分区时C点的速度范围,再由动能定理求解即可.
解答  解:(1)小球离开C点时做平抛运动,则有:
解:(1)小球离开C点时做平抛运动,则有:
2R=$\frac{1}{2}g{t}^{2}$
d=vC1t
联立解得:vC1=2m/s
(2)设轨道对小球的作用力大小为F,则在C点有:
mg+F=m$\frac{{v}_{C1}^{2}}{R}$
解得:F=0
(3)小球落在N点,经过C点的速度为:vC1=$\frac{d+△d}{t}$=3m/s
所以小球要落在得分区,经过C点的速度大小范围为:2m/s≤vC≤3m/s
从小球释放滑到C点,根据动能定理得:
mg(xsinθ-2R)-μmgxcosθ=$\frac{1}{2}m{v}_{C}^{2}$
联立以上式子,得:$\sqrt{3}$m≤x≤$\frac{5\sqrt{3}}{4}$m
所以小球在杆上离B点$\sqrt{3}$m~$\frac{5\sqrt{3}}{4}$m的距离处释放才能落在得分区.
答:(1)小球离开C点时的速度是2m/s才能落在得分区的M点.
(2)落在M点的小球在C处时,轨道对小球的作用力是0.
(3)若θ=60°,小球在杆上离B点$\sqrt{3}$m~$\frac{5\sqrt{3}}{4}$m的距离距离处释放才能落在得分区.
点评 对于平抛运动,要熟练运用运动的分解法研究,要知道平抛运动的时间由下落的高度决定的,高度一定时下落时间是相等的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列属于国际单位制中基本单位的一组是( )
| A. | 米、千克、秒 | B. | 长度、质量、时间 | C. | 位移、速度、力 | D. | 米、米/秒、牛顿 |
3.下列说法正确的是( )
| A. | 液体达到饱和气压时,蒸发停止,没有分子从液体表面蒸发出来 | |
| B. | 若分子间距增大,则分子间的斥力变小引力变大 | |
| C. | 一定质量的某理想气体,在温度升高时其内能一定增大 | |
| D. | 一滴液态金属在完全失重条件下呈球状,是由液体的表面张力所致 |
11. 如图甲所示,某空间存在着垂直于纸面向里的匀强磁场.磁场中A、B两个物块叠放在一起,置于光滑水平面上.物块A带正电,物块B不带电且表面绝缘.在t=0时刻,将一水平恒力F作用在物块B上,使物块A、B一起由静止开始做匀加速直线运动,图乙反映的可能是( )
如图甲所示,某空间存在着垂直于纸面向里的匀强磁场.磁场中A、B两个物块叠放在一起,置于光滑水平面上.物块A带正电,物块B不带电且表面绝缘.在t=0时刻,将一水平恒力F作用在物块B上,使物块A、B一起由静止开始做匀加速直线运动,图乙反映的可能是( )
 如图甲所示,某空间存在着垂直于纸面向里的匀强磁场.磁场中A、B两个物块叠放在一起,置于光滑水平面上.物块A带正电,物块B不带电且表面绝缘.在t=0时刻,将一水平恒力F作用在物块B上,使物块A、B一起由静止开始做匀加速直线运动,图乙反映的可能是( )
如图甲所示,某空间存在着垂直于纸面向里的匀强磁场.磁场中A、B两个物块叠放在一起,置于光滑水平面上.物块A带正电,物块B不带电且表面绝缘.在t=0时刻,将一水平恒力F作用在物块B上,使物块A、B一起由静止开始做匀加速直线运动,图乙反映的可能是( )| A. | 物块A的动能大小随时间t变化的关系 | |
| B. | 物块B对地面压力大小随时间t变化的关系 | |
| C. | 物块A所受洛伦兹力大小随时间t变化的关系 | |
| D. | 物块A对物块B的摩擦力大小随时间t变化的关系 |

 如图所示,粗糙的水平轨道AB与竖直放置的半圆形光滑轨道在B点相切连接,AB段长x=4$\sqrt{2}$m,半圆形轨道半径R=2m,质量m=1kg的小滑块(可视为质点)在F=100N的水平恒力作用下,从A点由静止开始运动,在小滑块到达B点之前撇去力F,小滑块沿轨道运动到最高点C后水平飞出,又恰好落回A点.已知滑块与水平轨道间的动摩擦因数μ=$\frac{\sqrt{2}}{2}$,重力加速度g取10m/s2.求:
如图所示,粗糙的水平轨道AB与竖直放置的半圆形光滑轨道在B点相切连接,AB段长x=4$\sqrt{2}$m,半圆形轨道半径R=2m,质量m=1kg的小滑块(可视为质点)在F=100N的水平恒力作用下,从A点由静止开始运动,在小滑块到达B点之前撇去力F,小滑块沿轨道运动到最高点C后水平飞出,又恰好落回A点.已知滑块与水平轨道间的动摩擦因数μ=$\frac{\sqrt{2}}{2}$,重力加速度g取10m/s2.求: