题目内容
9. 某课外探究小组的学生在表演“水流星”节目,如图所示,杯子可视为质点,拴杯子的绳长为L,绳子能承受的最大拉力是杯子和杯内水总重力的10倍,重力加速度为g,要使绳子不断裂,节目成功,则杯子通过最高点的速度最小为$\sqrt{gL}$,通过最低点的速度最大为$3\sqrt{gL}$.
某课外探究小组的学生在表演“水流星”节目,如图所示,杯子可视为质点,拴杯子的绳长为L,绳子能承受的最大拉力是杯子和杯内水总重力的10倍,重力加速度为g,要使绳子不断裂,节目成功,则杯子通过最高点的速度最小为$\sqrt{gL}$,通过最低点的速度最大为$3\sqrt{gL}$.
分析 对水分析,在最高点,当杯子对水的弹力为零时,速度最小,根据牛顿第二定律求出速度的最小值.
在最低点绳子有最大拉力,根据牛顿第二定律求出在最低点速度的最大值.
解答 解:在最高点,临界情况是桶底对水的弹力为零.有:
mg=m$\frac{{v}^{2}}{L}$
解得:v=$\sqrt{gL}$.
在最低点绳子的最大拉力为10mg,则有:
T-mg=m$\frac{v{′}^{2}}{L}$
解得:v′=3$\sqrt{gL}$.
故答案为:$\sqrt{gL}$,3$\sqrt{gL}$
点评 解决本题的关键知道物体做圆周运动向心力的来源,知道“绳模型”的临界情况,根据牛顿第二定律进行求解.

练习册系列答案
相关题目
3. 如图所示,一倾角为θ=30°的传送带以速度v沿顺时针方向匀速率运动,现将一物块由静止释放在传送带的最下端(现将一物体由传送带最下端静止释放),物块到达传送带最上端时恰好与传送带速度相等,则物块在传送带上运动的平均速度为( )
如图所示,一倾角为θ=30°的传送带以速度v沿顺时针方向匀速率运动,现将一物块由静止释放在传送带的最下端(现将一物体由传送带最下端静止释放),物块到达传送带最上端时恰好与传送带速度相等,则物块在传送带上运动的平均速度为( )
 如图所示,一倾角为θ=30°的传送带以速度v沿顺时针方向匀速率运动,现将一物块由静止释放在传送带的最下端(现将一物体由传送带最下端静止释放),物块到达传送带最上端时恰好与传送带速度相等,则物块在传送带上运动的平均速度为( )
如图所示,一倾角为θ=30°的传送带以速度v沿顺时针方向匀速率运动,现将一物块由静止释放在传送带的最下端(现将一物体由传送带最下端静止释放),物块到达传送带最上端时恰好与传送带速度相等,则物块在传送带上运动的平均速度为( )| A. | $\frac{\sqrt{3}}{3}$v | B. | $\frac{1}{2}$v | C. | $\frac{\sqrt{3}}{2}$v | D. | v |
17.某人造卫星因受高空稀薄空气的阻力作用绕地球运动的轨道会慢慢减小,每次测量中,卫星的运动均可近似看作圆周运动,则它受到的万有引力、线速度及运动周期的变化情况是( )
| A. | 变大、变小、变大 | B. | 变小、变大、变小 | C. | 变小、变小、变大 | D. | 变大、变大、变小 |
4. 如图所示,A、B、C是同一轨道平面上的三颗人造地球卫星,忽略三颗卫星之间的万有引力,关于三颗卫星对应的相关物理量的大小比较,下列判断正确的是( )
如图所示,A、B、C是同一轨道平面上的三颗人造地球卫星,忽略三颗卫星之间的万有引力,关于三颗卫星对应的相关物理量的大小比较,下列判断正确的是( )
 如图所示,A、B、C是同一轨道平面上的三颗人造地球卫星,忽略三颗卫星之间的万有引力,关于三颗卫星对应的相关物理量的大小比较,下列判断正确的是( )
如图所示,A、B、C是同一轨道平面上的三颗人造地球卫星,忽略三颗卫星之间的万有引力,关于三颗卫星对应的相关物理量的大小比较,下列判断正确的是( )| A. | 线速度大小vA<vB<vC | B. | 万有引力大小FA>FB>FC | ||
| C. | 角速度的大小ωA>ωB>ωC | D. | 向心加速度大小aA<aB<aC |
14.关于平抛运动,下列说法中正确的是( )
| A. | 平抛运动的轨迹是曲线,所以平抛运动是变加速运动 | |
| B. | 平抛运动是一种匀变速曲线运动 | |
| C. | 平抛运动的水平射程s仅由初速度v0决定,v0越大,s越大 | |
| D. | 水平飞行的时间只与抛出点的高度和水平速度有关 |
1.一颗人造卫星在绕地球做匀速圆周运动,其轨道半径为地球半径的 3 倍,则该卫星做匀速圆周运动的速度( )
| A. | 一定等于7.9km/s | B. | 一定小于7.9km/s | ||
| C. | 一定大于7.9km/s | D. | 介于7.9 km/s~7.9 km/s |
18. 如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )
如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )
 如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )
如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )| A. | 小球抛出时的速度大小为gtcotθ | |
| B. | 小球刚落到斜面上时的速度大小为$\frac{gt}{tan\;θ}$ | |
| C. | 小球的位移与竖直方向夹角的正切值为2cotθ | |
| D. | 水平分位移与竖直分位移之比为2tanθ |
19.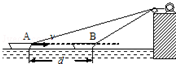 如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )
如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )
 如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )
如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )| A. | 小船经过B点时的速度大小为VB=$\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}$ | |
| B. | 小船经过B点时绳子对小船的拉力大小为$\frac{Pcosθ}{\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}}$ | |
| C. | 小船经过A点时电动机牵引绳子的速度大小为$\frac{v}{cosθ}$ | |
| D. | 小船经过B点时的加速度大小为$\frac{P}{\sqrt{{m}^{2}{v}^{2}+2m(Pt-fd)}}$-$\frac{f}{m}$ |
 某同学在室内进行抛接小球练习,小球抛接点固定在同一位置,如图所示,第一次小球竖直上抛的初速度为8m/s,小球恰好没有碰到天花板,该同学成功接住小球;第二次将小球以10m/s的初速度竖直抛出,该同学又成功接住小球.已知小球与天花板碰撞前后速度大小不变,小球与天花板碰撞的时间忽略不计,小球运动时的空气阻力不计,小球可视为质点,重力加速度g=10m/s2.求:
某同学在室内进行抛接小球练习,小球抛接点固定在同一位置,如图所示,第一次小球竖直上抛的初速度为8m/s,小球恰好没有碰到天花板,该同学成功接住小球;第二次将小球以10m/s的初速度竖直抛出,该同学又成功接住小球.已知小球与天花板碰撞前后速度大小不变,小球与天花板碰撞的时间忽略不计,小球运动时的空气阻力不计,小球可视为质点,重力加速度g=10m/s2.求: