题目内容
1．
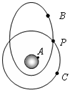如图所示，A为地球赤道上随地球自转的物体，B为绕地球做椭圆轨道运行的卫星，C为绕地球做圆周运动的卫星，P为B、C两卫星轨道的交点．已知A、B、C绕地心运动的周期都相同，则（ ）| A． | 相对于地心，卫星C的运行速度大于物体A的速度 | |
| B． | 相对于地心，卫星C的运行角速度等于物体A的角速度 | |
| C． | 卫星B在P点的加速度大小等于卫星C在该点加速度大小 | |
| D． | 卫星B在P点通过加速进入卫星C所在轨道运行 |
分析 根据A、C的周期相等，知角速度相等，通过v=rω比较A、C速度的大小．因为卫星的周期一定，根据万有引力提供向心力确定其轨道半径一定．根据卫星所受的万有引力，通过牛顿第二定律比较加速度的大小．
解答 解：A、物体A和卫星C的周期相等，则角速度相等，根据v=rω知，半径越大，线速度越大．所以卫星C的运行速度大于物体A的速度．故A正确，B正确；
C、根据a=$\frac{F}{m}$=$G\frac{M}{{r}_{\;}^{2}}$知，两卫星距离地心的距离相等，则加速度相等．故C正确，
D、卫星B在P点通过加速会做离心运动，不可能进入卫星C所在的轨道运行，故D错误
故选：ABC
点评 解决本题的关键知道A和C的角速度相等，通过v=rω 比较线速度大小，注意物体A随地球做圆周运动不是靠万有引力提供向心力．
练习册系列答案
考前必练系列答案
相关题目
12．下列说法正确的是（ ）
| A． | 参考系必须是固定不动的物体 | |
| B． | 第3 s末是指一个时刻 | |
| C． | 地球很大，又有自转，研究地球公转时，地球不可视为质点 | |
| D． | 在直线运动中，质点位移的大小一定等于其路程 |
6．若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球，测出小球的水平射程为L．已知月球半径为R，万有引力常量为G．则下列说法正确的是（ ）
| A． | 月球表面的重力加速度g月=$\frac{2h{{v}_{0}}^{2}}{{L}^{2}}$ | |
| B． | 月球的质量g月=$\frac{2h{R}^{2}{{v}_{0}}^{2}}{G{L}^{2}}$ | |
| C． | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2hR}$ | |
| D． | 月球的平均密度ρ=$\frac{3h{{v}_{0}}^{2}}{2πG{L}^{2}}$ |
如图为某次太空探测中，科研人员发射星球探测器在最后着陆阶段的示意图，探测器在距星球表面高度为H=20m处悬停（速度为0），首先使探测器在重力作用下自由下落，下落到距地表h高度处开启发动机，使探测器竖直匀减速下降．不计星球表面大气对探测器的阻力影响，星球表面附近的重力加速度为g0=4m/s2．求：
4．
某杂枝演员在做手指玩耍盘高难度的表演，如图所示．设该盘的质量为m，手指与盘之间的滑动摩擦因数为?，重力加速度为g，设最大静摩擦等于滑动摩擦，盘底处于水平状态且不考虑盘的自转，则下列说法中正确的是（ ）
某杂枝演员在做手指玩耍盘高难度的表演，如图所示．设该盘的质量为m，手指与盘之间的滑动摩擦因数为?，重力加速度为g，设最大静摩擦等于滑动摩擦，盘底处于水平状态且不考虑盘的自转，则下列说法中正确的是（ ）| A． | 若手指支撑着盘，使盘保持静止状态，则手指对盘的作用力大于mg | |
| B． | 若手指支撑着盘并一起水平向右匀速运动，则盘水平向右的静摩擦力 | |
| C． | 若手指支撑着盘并一起水平向右匀加速运动，则手对盘的作用力大小为μmg | |
| D． | 若盘随手指一起水平匀加速运动，则手对盘的作用力大小不可超过$\sqrt{1+{μ}^{2}}$mg |
5．一辆汽车正在做匀加速直线运动，计时之初，速度为6m/s，运动28m后速度增加到8m/s，则（ ）
| A． | 这段运动所用时间是4 s | |
| B． | 这段运动的加速度是3.5 m/s2 | |
| C． | 自开始计时起，两秒末的速度是7 m/s | |
| D． | 从开始计时起，经过14 m处的速度是5 m/s |