��Ŀ����
8�� ��ͼ��ʾ������ֱֽ���������ǿ�ų���MNΪ�߽磬MN�߽��Ϸ��Ÿ�Ӧǿ�ȴ�СB1�����·��ų��ĴŸ�Ӧǿ�ȴ�СB2��δ֪������һ��Ϊl��ƽֱ������MN�غϣ�һ�Ⱥ�Ϊc�Ĵ��������Ӵӵ�����е�O���ش�ֱ���巽�����ٶ�v=$\frac{c{B}_{1}l}{k}$��kΪż���������Ϸ��ų��У����������뵲�巢����ײ����������û��������ʧ�����������·��ų����˶�ʱ�����뵲�淢����ײ�����������ܻص�������O������������������k=4�������Ӵӵ����Ե�����·��ų��У�
��ͼ��ʾ������ֱֽ���������ǿ�ų���MNΪ�߽磬MN�߽��Ϸ��Ÿ�Ӧǿ�ȴ�СB1�����·��ų��ĴŸ�Ӧǿ�ȴ�СB2��δ֪������һ��Ϊl��ƽֱ������MN�غϣ�һ�Ⱥ�Ϊc�Ĵ��������Ӵӵ�����е�O���ش�ֱ���巽�����ٶ�v=$\frac{c{B}_{1}l}{k}$��kΪż���������Ϸ��ų��У����������뵲�巢����ײ����������û��������ʧ�����������·��ų����˶�ʱ�����뵲�淢����ײ�����������ܻص�������O������������������k=4�������Ӵӵ����Ե�����·��ų��У���1���Ի���k=10ʱ���ӵ��˶��켣��
��2�������ų��ĴŸ�Ӧǿ�ȴ�С�ı�ֵ$\frac{{B}_{1}}{{B}_{2}}$��
���� ��1���������������ṩ����������뾶�������켣
��2��k=4ʱ���������´ų����˶��Ĺ켣���õ��뾶֮��Ĺ�ϵ���Ӷ���ôŸ�Ӧǿ��֮��
��� �⣺��1�����Ӵ�O������Ϸ��ų������������ṩ������������ţ�ٵڶ�����$qvB=m\frac{{v}_{\;}^{2}}{R}$����$R=\frac{mv}{qB}$
���Ϸ��ų��У��뾶${R}_{1}^{\;}=\frac{mv}{q{B}_{1}^{\;}}$=$\frac{1}{c{B}_{1}}•\frac{c{B}_{1}l}{k}$=$\frac{l}{k}$
��k=10ʱ��$v=\frac{c{B}_{1}^{\;}l}{k}=\frac{c{B}_{1}^{\;}l}{10}$
�������Ϸ��ų���������Բ���˶��İ뾶${R}_{1}^{��}=\frac{mv}{q{B}_{1}^{\;}}=\frac{l}{10}$���켣��ͼ��ʾ��
��2���������·��ų����˶�ʱ���켣�뾶${R}_{2}^{\;}=\frac{mv}{q{B}_{2}^{\;}}$=$\frac{1}{c{B}_{2}}•\frac{c{B}_{1}l}{k}$=$\frac{{B}_{1}l}{k{B}_{2}}$��
�����ӳ�����n����Բ�켣����MN�·��ų����ɼ��ι�ϵ�ɵ�4��n-1��R1��l��4R1��
��4nR1=2R2��
��$\frac{{B}_{1}}{{B}_{2}}$=2n��Ϊż����$\frac{k}{2}$��$\frac{{B}_{1}}{{B}_{2}}$��$\frac{k}{2}$+2��
����kΪż������$\frac{{B}_{1}}{{B}_{2}}$=$\frac{k}{2}$��$\frac{k}{2}$+1��
��k����4�ı���ʱ��$\frac{{B}_{1}}{{B}_{2}}$=$\frac{k}{2}$��
��k������4�ı���ʱ��$\frac{{B}_{1}}{{B}_{2}}$=$\frac{k}{2}$+1��
�𣺣�1��k=10ʱ���ӵ��˶��켣����ͼ��
��2����k����4�ı���ʱ��$\frac{{B}_{1}}{{B}_{2}}$=$\frac{k}{2}$����k������4�ı���ʱ��$\frac{{B}_{1}}{{B}_{2}}$=$\frac{k}{2}$+1��
���� ������Ŀ��ӱ���д��⣬����Ļ���˼�벻�䣬����ԭ�����������ṩ����������뾶��ȷ��Բ�ģ������켣��

 ����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������| A�� | A�нӵ��ǵ��裬B�нӵ��ǵ����� | |
| B�� | A�нӵ��ǵ�������B�нӵ��ǵ����Ȧ | |
| C�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ����� | |
| D�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ��� |
 �����ڹ�������������ʻ���������ɹ��ŵ���ߵ�A��ʻ����͵�B�Ĺ����У�����˵������ȷ���ǣ�������
�����ڹ�������������ʻ���������ɹ��ŵ���ߵ�A��ʻ����͵�B�Ĺ����У�����˵������ȷ���ǣ�������| A�� | ֧���������� | B�� | ���������� | C�� | Ħ���������� | D�� | ǣ���������� |
| A�� | ����������ЧӦ��ԭ���ǹ۲��ߵ���������������ԭ�� | |
| B�� | ����������������Ƶ��Խ�����������һ��Խ�� | |
| C�� | �ڸ��������У���ǿ���λ�ƿ��ܱ��������λ��С | |
| D�� | �ڵ�����������г�˶��Ļظ�������ʽF=-kx�У�FΪ�������ܵ��ĺ�������kΪ���ɵľ���ϵ�� | |
| E�� | �ڻ�е���Ĵ��������У��ʵ���һ�����ڣ��ͻ��ڽ������ز��Ĵ�������һ�������ľ��� |
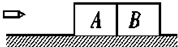 ��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ����������Ӵ���ľ��A��B�������ֱ�Ϊm 1��m 2������һ�ӵ�ˮƽ������ľ�飮���ӵ�����ľ��A��B��ʱ��ֱ�Ϊt1��t2��ľ����ӵ���������Ϊf�����ӵ�������ľ���ľ��A��B���ٶȴ�С�ֱ��ǣ�������
��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ����������Ӵ���ľ��A��B�������ֱ�Ϊm 1��m 2������һ�ӵ�ˮƽ������ľ�飮���ӵ�����ľ��A��B��ʱ��ֱ�Ϊt1��t2��ľ����ӵ���������Ϊf�����ӵ�������ľ���ľ��A��B���ٶȴ�С�ֱ��ǣ�������| A�� | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ | |
| B�� | $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$+$\frac{f{t}_{2}}{{m}_{2}}$ | |
| C�� | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}+{m}_{2}}$ | |
| D�� | $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}}$ $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}+{m}_{2}}$ |
 ����Ϊm����飬���Ű뾶ΪR�İ����ν������ڱڻ��£������ν�������ֱ���ã��������ϣ�������͵�ʱ�ٶȴ�СΪv�������������֮���Ħ������Ϊ�̣�����������͵�ʱ������˵����ȷ���ǣ�������
����Ϊm����飬���Ű뾶ΪR�İ����ν������ڱڻ��£������ν�������ֱ���ã��������ϣ�������͵�ʱ�ٶȴ�СΪv�������������֮���Ħ������Ϊ�̣�����������͵�ʱ������˵����ȷ���ǣ�������| A�� | �ܵ���������СΪmg+m$\frac{{v}^{2}}{R}$ | B�� | �ܵ�֧����Ϊmg+m$\frac{{v}^{2}}{R}$ | ||
| C�� | �ܵ���Ħ����Ϊ��mg | D�� | �ܵ���Ħ����Ϊ��m$\frac{{v}^{2}}{R}$ |

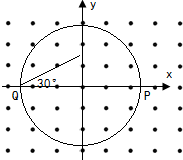 ��ͼ��ʾ����ֱ������ϵx0y�ڣ���ԭ��0ΪԲ�ģ��뾶ΪR��Բ�������ڴ����Ŵ�ֱֽ���������ǿ�ų���һ�����Ӵ�P�㣨R��0����x�Ḻ����������v����ų����ڴų����˶���ʱ��Ϊt1��һ�����Ӵ�Q�㣨-R��0��������x�������30��ķ���������2v����ų���ǡ�ô�P��ɳ��ų����ڴų����˶���ʱ��Ϊt2�����������������������������t1��t2Ϊ��������
��ͼ��ʾ����ֱ������ϵx0y�ڣ���ԭ��0ΪԲ�ģ��뾶ΪR��Բ�������ڴ����Ŵ�ֱֽ���������ǿ�ų���һ�����Ӵ�P�㣨R��0����x�Ḻ����������v����ų����ڴų����˶���ʱ��Ϊt1��һ�����Ӵ�Q�㣨-R��0��������x�������30��ķ���������2v����ų���ǡ�ô�P��ɳ��ų����ڴų����˶���ʱ��Ϊt2�����������������������������t1��t2Ϊ��������