题目内容
1. 如图所示,充电后的平行板电容器水平放置,电容为C,极板间的距离为d,上板正中有一小孔.质量为m、电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g).求:
如图所示,充电后的平行板电容器水平放置,电容为C,极板间的距离为d,上板正中有一小孔.质量为m、电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g).求:(1)小球到达小孔处的速度;
(2)极板间电场强度的大小和电容器所带电荷量;
(3)小球从开始下落运动到下极板处的时间.
分析 (1)小球到达小孔前是自由落体运动,根据速度位移关系公式列式求解即可;
(2)对从释放到到达下极板处过程运用动能定理列式求解电场强度,然后根据Q=CU求解电容器的带电量;
(3)对加速过程和减速过程分别运用动量定理列式求解时间,然后求和即可.
解答 解:(1)由${v}_{\;}^{2}=2gh$
解得:$v=\sqrt{2gh}$
(2)对从释放到到达下极板处过程运用动能定理列式,有:
mg(h+d)-qEd=0
得$E=\frac{mg(h+d)}{qd}$
电容器两极板间的电压为:U=Ed
电容器所带电荷量Q=CU
得$Q=C\frac{mg(h+d)}{q}$
(3)加速过程:
mgt1=mv…③
减速过程,有:
(mg-qE)t2=0-mv…④
t=t1+t2…⑤
联立①②③④⑤解得:
t=$\frac{h+d}{h}\sqrt{\frac{2h}{g}}$
答:(1)小球到达小孔处的速度为$\sqrt{2gh}$;
(2)极板间电场强度大小为$\frac{mg(h+d)}{qd}$,电容器所带电荷量为$\frac{mg(h+d)C}{q}$;
(3)小球从开始下落运动到下极板处的时间为$\frac{h+d}{h}\sqrt{\frac{2h}{g}}$.
点评 本题关键是明确小球的受力情况和运动规律,然后结合动能定理和动量定理列式分析,不难.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
6.如图所示,表示物体作匀减速直线运动的图象是( )
| A. |  | B. |  | C. |  | D. |  |
7.一辆汽车以10m/s的速度沿平直公路匀速运动,司机发现前方有障碍物立即减速,以0.2m/s2的加速度做匀减速运动,开始减速后一分钟内汽车的位移为( )
| A. | 240m | B. | 250m | C. | 600m | D. | 840m |
6. 如图所示,质量为m、边长为L、回路电阻为R的正方形金属框,用细线吊住,放在光滑的倾角为30°的斜面上,线的另一端跨过两个定滑轮,挂着一个质量为M(M>m)的砝码,金属框沿斜面上方有一磁感应强度为B的匀强磁场,磁场的下边界与金属框的上边平行且相距一定距离.则在金属框从开始运动到整个框进入磁场的过程中,下列说法正确的是( )
如图所示,质量为m、边长为L、回路电阻为R的正方形金属框,用细线吊住,放在光滑的倾角为30°的斜面上,线的另一端跨过两个定滑轮,挂着一个质量为M(M>m)的砝码,金属框沿斜面上方有一磁感应强度为B的匀强磁场,磁场的下边界与金属框的上边平行且相距一定距离.则在金属框从开始运动到整个框进入磁场的过程中,下列说法正确的是( )
 如图所示,质量为m、边长为L、回路电阻为R的正方形金属框,用细线吊住,放在光滑的倾角为30°的斜面上,线的另一端跨过两个定滑轮,挂着一个质量为M(M>m)的砝码,金属框沿斜面上方有一磁感应强度为B的匀强磁场,磁场的下边界与金属框的上边平行且相距一定距离.则在金属框从开始运动到整个框进入磁场的过程中,下列说法正确的是( )
如图所示,质量为m、边长为L、回路电阻为R的正方形金属框,用细线吊住,放在光滑的倾角为30°的斜面上,线的另一端跨过两个定滑轮,挂着一个质量为M(M>m)的砝码,金属框沿斜面上方有一磁感应强度为B的匀强磁场,磁场的下边界与金属框的上边平行且相距一定距离.则在金属框从开始运动到整个框进入磁场的过程中,下列说法正确的是( )| A. | 细线对金属框做的功等于金属框增加的机械能 | |
| B. | 细线对金属框的拉力可能等于Mg | |
| C. | 线框上的热功率可能大于$\frac{(M-o.5m)^{2}{g}^{2}R}{{B}^{2}{L}^{2}}$ | |
| D. | 如线框加速进入磁场,系统的机械能损失可能小于MgL-$\frac{1}{2}$mgL |
11. 小明同学正在做这样一道物理题:如图所示,轻绳一端系着一个质量为m的小球A,将轻绳另一端悬挂于O点,若在小球上施加一个水平的作用力F,使轻绳偏离竖直方向,与竖直方向成θ角,此时水平作用力F的大小为多少?小明同学思考:若将轻绳改为绝缘丝线,并让小球带上电荷量为q的正电荷,然后在此空间加上一个匀强电场去实现上述偏离目标,那么这个电场的电场强度最小值E与F的比值为( )
小明同学正在做这样一道物理题:如图所示,轻绳一端系着一个质量为m的小球A,将轻绳另一端悬挂于O点,若在小球上施加一个水平的作用力F,使轻绳偏离竖直方向,与竖直方向成θ角,此时水平作用力F的大小为多少?小明同学思考:若将轻绳改为绝缘丝线,并让小球带上电荷量为q的正电荷,然后在此空间加上一个匀强电场去实现上述偏离目标,那么这个电场的电场强度最小值E与F的比值为( )
 小明同学正在做这样一道物理题:如图所示,轻绳一端系着一个质量为m的小球A,将轻绳另一端悬挂于O点,若在小球上施加一个水平的作用力F,使轻绳偏离竖直方向,与竖直方向成θ角,此时水平作用力F的大小为多少?小明同学思考:若将轻绳改为绝缘丝线,并让小球带上电荷量为q的正电荷,然后在此空间加上一个匀强电场去实现上述偏离目标,那么这个电场的电场强度最小值E与F的比值为( )
小明同学正在做这样一道物理题:如图所示,轻绳一端系着一个质量为m的小球A,将轻绳另一端悬挂于O点,若在小球上施加一个水平的作用力F,使轻绳偏离竖直方向,与竖直方向成θ角,此时水平作用力F的大小为多少?小明同学思考:若将轻绳改为绝缘丝线,并让小球带上电荷量为q的正电荷,然后在此空间加上一个匀强电场去实现上述偏离目标,那么这个电场的电场强度最小值E与F的比值为( )| A. | qtanθ | B. | qsinθ | C. | $\frac{q}{cosθ}$ | D. | $\frac{cosθ}{q}$ |
 如图,已知O点受两个力F1和F2作用,F1=3N,F2=4N,F1沿①所指的方向作用,F2沿②所指的方向作用,根据图上所给的标度分别画出F1和F2的力的图示.利用作图法在图上画出F1和F2的合力F,根据作图的结果求出合力F的大小,并将所求的F大小填在图中的空格内.利用作图法得出的合力F=5.9N.
如图,已知O点受两个力F1和F2作用,F1=3N,F2=4N,F1沿①所指的方向作用,F2沿②所指的方向作用,根据图上所给的标度分别画出F1和F2的力的图示.利用作图法在图上画出F1和F2的合力F,根据作图的结果求出合力F的大小,并将所求的F大小填在图中的空格内.利用作图法得出的合力F=5.9N.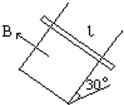 如图所示,金属框架与水平面成30°角,匀强磁场的磁感强度B=0.4T,方向垂直框架平面向上,金属棒长l=0.5m,重量为0.1N,可以在框架上无摩擦地滑动,棒与框架的总电阻为2Ω,运动时可认为不变,导体棒刚开始距离地面2m,问:
如图所示,金属框架与水平面成30°角,匀强磁场的磁感强度B=0.4T,方向垂直框架平面向上,金属棒长l=0.5m,重量为0.1N,可以在框架上无摩擦地滑动,棒与框架的总电阻为2Ω,运动时可认为不变,导体棒刚开始距离地面2m,问: