题目内容
15.一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ.初始时,传送带与煤块都是静止的.现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动.求:(1)传送带从静止开始加速到v0所需的时间;
(2)从传送带开始运动到速度刚达到v0这段时间内,煤块相对地面的位移大小;
(3)煤块在传送带上留下黑色痕迹的长度.
分析 传送带先加速后匀速,煤块先加速,当速度增大到等于传送带速度后,与传送带不再相对滑动,一起匀速.先根据牛顿第二定律求出加速度,再根据运动学公式计算出运动时间,求出煤块和皮带的位移后,即可以得到黑色痕迹的长度.
解答 解:(1)设经历时间t,传送带由静止开始加速到速度等于v0,v0=a0t 所以,t=$\frac{{v}_{0}}{{a}_{0}}$
(2)煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0.根据牛顿定律,可得a=μg
则当传送带速度刚达到v0时,煤块相对地面运动的位移为
s1=$\frac{1}{2}$at2=$\frac{1}{2}$μg($\frac{{v}_{0}}{a}$)2=$\frac{μg{v}_{0}^{2}}{2{a}_{0}^{2}}$
(3)设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s,有
s0=$\frac{1}{2}$a0t2+v0t′
s=$\frac{{v}_{0}^{2}}{2a}$
传送带上留下的黑色痕迹的长度
l=s0-s
由以上各式得
黑色痕迹的长度l=$\frac{{v}_{0}^{2}{(a}_{0}-μg)}{2{μa}_{0}g}$;
答:(1)传送带从静止开始加速到v0所需的时间为$\frac{{v}_{0}}{{a}_{0}}$;
(2)从传送带开始运动到速度刚达到v0这段时间内,煤块相对地面的位移大小为$\frac{μg{v}_{0}^{2}}{2{a}_{0}^{2}}$;
(3)煤块在传送带上留下黑色痕迹的长度为$\frac{{v}_{0}^{2}{(a}_{0}-μg)}{2{μa}_{0}g}$.
点评 本题关键分析清楚皮带和煤块的受力情况和运动情况,要做好受力分析和过程分析,然后根据运动学公式求解.

 阅读快车系列答案
阅读快车系列答案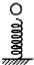 如图所示,自由下落的小球落向竖直放置的弹簧,然后沿弹簧轴线向下压缩弹簧.从小球接触弹簧开始到弹簧被压缩到最短的过程中,小球的速度和加速度大小的变化情况是( )
如图所示,自由下落的小球落向竖直放置的弹簧,然后沿弹簧轴线向下压缩弹簧.从小球接触弹簧开始到弹簧被压缩到最短的过程中,小球的速度和加速度大小的变化情况是( )| A. | 加速度一直变小,速度一直变小 | |
| B. | 加速度一直变大,速度一直变小 | |
| C. | 加速度先变小后变大,速度先变大后变小 | |
| D. | 加速度先变大后变小,速度先变大后变小 |
 如图甲所示,一对光滑的平行导轨(电阻不计)固定在同一水平面,导轨足够长且间距L=0.5m.左端接有阻值为R=4Ω的电阻,一质量为m=1kg长度也为L的金属棒MN放置在导轨上,金属棒MN的电阻r=1Ω,整个装置置于方向竖直向上的匀强磁场中,金属棒在水平向右的外力F的作用下由静止开始运动,拉力F与金属棒的速率的倒数关系如图乙,则( )
如图甲所示,一对光滑的平行导轨(电阻不计)固定在同一水平面,导轨足够长且间距L=0.5m.左端接有阻值为R=4Ω的电阻,一质量为m=1kg长度也为L的金属棒MN放置在导轨上,金属棒MN的电阻r=1Ω,整个装置置于方向竖直向上的匀强磁场中,金属棒在水平向右的外力F的作用下由静止开始运动,拉力F与金属棒的速率的倒数关系如图乙,则( )| A. | 拉力F的功率逐渐增大 | |
| B. | v=5m/s时拉力的功率为20W | |
| C. | 磁场的磁感应强度为2.0T | |
| D. | 若经过时间t=4s金属棒达到最大速度,则在这段时间内电阻R产生的热量为30J |

| A. | A、B两点的电场强度大小不等,方向相同 | |
| B. | A、B两点的电场强度大小相等,方向不同 | |
| C. | 左边电荷带负电,右边电荷带正电 | |
| D. | 两电荷所带电荷量相等 |
| A. | 手机可能只受到压力和重力作用 | |
| B. | 手机可能只受到摩擦力和重力作用 | |
| C. | 手机一定受到摩擦力、压力、重力作用 | |
| D. | 手机一定受到摩擦力、手臂的举力、压力、重力作用 |
 如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表
如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表 的示数减小△U(电压表为理想电表),在这个过程中( )
的示数减小△U(电压表为理想电表),在这个过程中( )| A. | R2两端的电压增加,增加量一定等于△U | |
| B. | 流过R的电流会减小 | |
| C. | 路端电压减小,减少量一定等于△U | |
| D. | △U和干路电流的变化△I的比值保持不变 |