题目内容
4.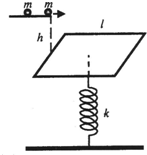 如图所示,质量为m,边长为l的正方形平板与弹簧相连,弹簧的劲度系数为k,另一端固定于地面,平板处于平衡状态.质量为m的第一个小球从平台以一定速度垂直于平板的左边缘水平抛出,并与平板发生完全非弹性碰撞(设平台与板间高度差为h,抛出点在平板的左边缘正上方).隔一段时间后,以相同速度抛出第二个小球.(假定在任何情况下平板始终保持水平,忽略平板在水平方向上的运动,且为方便计算起见,设h=3$\frac{mg}{k}$)
如图所示,质量为m,边长为l的正方形平板与弹簧相连,弹簧的劲度系数为k,另一端固定于地面,平板处于平衡状态.质量为m的第一个小球从平台以一定速度垂直于平板的左边缘水平抛出,并与平板发生完全非弹性碰撞(设平台与板间高度差为h,抛出点在平板的左边缘正上方).隔一段时间后,以相同速度抛出第二个小球.(假定在任何情况下平板始终保持水平,忽略平板在水平方向上的运动,且为方便计算起见,设h=3$\frac{mg}{k}$)(1)求第一个小球落到平台上形成的振子系统的周期和频率;
(2)在第二个小球能与平板不发生碰撞的情况下,其抛出速度的最小值为多少?
(3)在(2)的情况下,两小球抛出的时间差是多少?
分析 (1)根据弹簧振子的周期公式T=2π$\sqrt{\frac{m}{k}}$,m是振子的质量,来求振子系统的周期,由f=$\frac{1}{T}$求频率.
(2)研究第一个球的运动过程:由平抛运动的规律求出小球落在木板上时竖直分速度,由动量守恒定律求出球与木板碰后的共同速度,从而得到振幅,根据旋转参考矢量与y轴负方向的夹角满足的条件求解.
(3)由下落的高度求出第一个小球下落到平板的时间.由简谐运动的规律求出碰撞后平板从原平衡位置压缩到最低位置的时间,结合周期性求解两小球抛出的时间差.
解答 解:(1)碰撞前后小球与平板(总质量为2m一起在新的平衡位置上下做简谐振动,如图中虚线所示,拢子系统的周期为 T=2π$\sqrt{\frac{2m}{k}}$
振子系统的频率为 γ=$\frac{1}{T}$=$\frac{1}{2π}$$\sqrt{\frac{k}{2m}}$
(2)碰撞前,第一个小球在竖直方向的速度为 vy=$\sqrt{2gh}$
发生完全弹性碰撞,竖直方向动量近似守恒,取向下为正方向,则有 mvy=2mvy′
则碰撞后平板运动的速度为 vy′=$\frac{1}{2}{v}_{y}$=$\sqrt{\frac{1}{2}gh}$
振子的角频率ω=$\frac{2π}{T}$=$\sqrt{\frac{k}{m}}$
振子振幅为 A=$\sqrt{\frac{({v}_{y}′)^{2}}{ω{\;}^{2}}+(\frac{mg}{k})^{2}}$=2$\frac{mg}{k}$
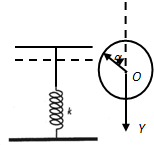
旋转参考矢量与y轴负方向的夹角满足
cosα=$\sqrt{\frac{mg}{mg+kh}}$=$\frac{1}{2}$,则 α=$\frac{π}{3}$
设析运动到最低点位置时第二个小球正好下落到这一高度,则第二个小球下落用时
t=$\sqrt{\frac{2(h+\frac{mg}{k}+A)}{g}}$=2$\sqrt{\frac{3m}{k}}$
由此可以求出两者不发生碰撞时,第二个小球的最小抛出速度为 v0=$\frac{l}{t}$=$\frac{l}{6}$$\sqrt{\frac{3k}{m}}$
(3)第一个小球下落到平板用时 t1=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{6m}{k}}$
碰撞后平板从原平衡位置压缩到最低位置用时 t2=$\frac{π-α}{ω}$=$\frac{2π}{3}$$\sqrt{\frac{2m}{k}}$
设两球抛出的时间相差△t,则△t+t=t1+t2
则得△t=t1+t2-t=$\sqrt{\frac{6m}{k}}$+$\frac{2π}{3}$$\sqrt{\frac{2m}{k}}$+2$\sqrt{\frac{3m}{k}}$
考虑到板往复一次用时T=2π$\sqrt{\frac{2m}{k}}$,第二个小球抛出时间可以是振子系统运动时间大于一个周期后,则两小球抛出的时间差为
△t=$\sqrt{\frac{6m}{k}}$+(2n+$\frac{2}{3}$)π$\sqrt{\frac{2m}{k}}$+2$\sqrt{\frac{3m}{k}}$(n取非负整数)
答:(1)第一个小球落到平台上形成的振子系统的周期为2π$\sqrt{\frac{2m}{k}}$,频率为$\frac{1}{2π}$$\sqrt{\frac{k}{2m}}$;
(2)在第二个小球能与平板不发生碰撞的情况下,其抛出速度的最小值为$\frac{l}{6}$$\sqrt{\frac{3k}{m}}$;
(3)在(2)的情况下,两小球抛出的时间差是$\sqrt{\frac{6m}{k}}$+(2n+$\frac{2}{3}$)π$\sqrt{\frac{2m}{k}}$+2$\sqrt{\frac{3m}{k}}$(n取非负整数).
点评 解决本题时要分析小球和振子的运动情况,掌握振子的周期公式,明确简谐运动的周期性,关键要分析隐含的临界条件.

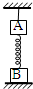 如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )
如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )| A. | 悬绳剪断瞬间,A物块的加速度大小为 1.5g | |
| B. | 悬绳剪断瞬间,A物块的加速度大小为g | |
| C. | 悬绳剪断后,A物块向下运动距离x时速度最大 | |
| D. | 悬绳剪断后,A物块向下运动距离3x时速度最大 |
 如图所示,平板车置于水平地面上,下列说法正确的是( )
如图所示,平板车置于水平地面上,下列说法正确的是( )| A. | 人站在平板车上保持静止时,人所受的重力和地面对平板车的支持力是一对平衡力 | |
| B. | 人站在平板车上保持静止时,平板车对人的支持力与平板车对地的压力是一对作用力和反作用力 | |
| C. | 人向上起跳加速阶段,平板车对人的支持力等于人对平板车的压力 | |
| D. | 人向上起跳加速阶段,人所受的重力等于人对平板车的压力 |
| A. | 速度相同 | B. | 速度不同 | C. | 频率相同 | D. | 频率不同 |
| A. | 1:1 | B. | 4:1 | C. | 1:16 | D. | 1:64 |
 如图所示,水平面上有一个物块,用一个与水平方向夹角为α的恒力F推着它做匀加速直线运动,一段时间后物块的位移为x,末速度为v,若此过程中F做的功为W,F做功的平均功率为$\overline{P}$,则( )
如图所示,水平面上有一个物块,用一个与水平方向夹角为α的恒力F推着它做匀加速直线运动,一段时间后物块的位移为x,末速度为v,若此过程中F做的功为W,F做功的平均功率为$\overline{P}$,则( )| A. | W=Fx | B. | $\overline{P}$=Fv | C. | W=Fxcosα | D. | $\overline{P}$=Fvcosα |
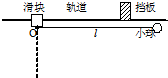 如图所示,滑块可以在水平放置的光滑固定长导轨上自由滑动,小球通过一不可伸缩的轻绳与滑块上的悬点O相连.滑块和小球的质量分别为m和2m,轻绳长为l,开始时,小球与滑块静止,且处于图示位置,轻绳呈水平拉直状态.
如图所示,滑块可以在水平放置的光滑固定长导轨上自由滑动,小球通过一不可伸缩的轻绳与滑块上的悬点O相连.滑块和小球的质量分别为m和2m,轻绳长为l,开始时,小球与滑块静止,且处于图示位置,轻绳呈水平拉直状态.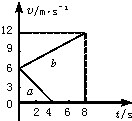 质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v-t图线.则图线b(填“a”或“b”)表示物体受拉力作用时的运动,该物体所受到的拉力是1.8N.
质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v-t图线.则图线b(填“a”或“b”)表示物体受拉力作用时的运动,该物体所受到的拉力是1.8N. 利用图示的装置来测量滑块A在长木板上运动的加速度.图中d为安装在滑块A上挡光片的宽度,s是1和2两个光电门之间的距离.实验时,使滑块A从长木板的顶端滑下.
利用图示的装置来测量滑块A在长木板上运动的加速度.图中d为安装在滑块A上挡光片的宽度,s是1和2两个光电门之间的距离.实验时,使滑块A从长木板的顶端滑下.