题目内容
9.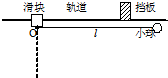 如图所示,滑块可以在水平放置的光滑固定长导轨上自由滑动,小球通过一不可伸缩的轻绳与滑块上的悬点O相连.滑块和小球的质量分别为m和2m,轻绳长为l,开始时,小球与滑块静止,且处于图示位置,轻绳呈水平拉直状态.
如图所示,滑块可以在水平放置的光滑固定长导轨上自由滑动,小球通过一不可伸缩的轻绳与滑块上的悬点O相连.滑块和小球的质量分别为m和2m,轻绳长为l,开始时,小球与滑块静止,且处于图示位置,轻绳呈水平拉直状态.(1)将小球由静止释放,若小球到达最低点时滑块刚好被一表面涂有强黏性物质的固定挡板极快地粘住.求:
(1-1)小球继续向左摆动达到最高点时,轻绳与竖直方向的夹角.
(1-2)挡板对滑块的冲量.
(1-3)小球从释放到第一次达到最低点的过程中,轻绳拉力对小球做的功.
(2)将小球由静止释放,若长轨道上无挡板,求小球在下落过程中速率的最大值.(本题可用TI图形计算器)
分析 (1)(1-1)小球由静止释放后的过程中,小球与滑块组成的系统水平方向不受外力,水平方向动量守恒,系统的机械能也守恒,由此列式求解小球到达最低点时的速度.小球到达最低点时滑块刚好被挡板极快地粘住,之后小球继续向左摆动达到最高点时,由机械能守恒定律求轻绳与竖直方向的夹角.
(1-2)由动量定理求挡板对滑块的冲量.
(1-3)由动能定理求轻绳拉力对小球做的功.
(2)若长轨道上无挡板,由动量守恒定律、机械能守恒定律和速度关系列式求解.
解答 解:(1-1)小球与滑块组成的系统水平方向无外力动量守恒,设小球与滑块达到最低点的速度分别为v1、v2,取水平向左为正方向,在小球下摆过程,由动量守恒定律有:
2mv1+mv2=0,得 2v1=-v2.
由机械能守恒定律有
$\frac{1}{2}$•2mv12+$\frac{1}{2}$mv22=2mgl,
解得:v12=$\frac{2}{3}$gl,v2=-2$\sqrt{\frac{2gl}{3}}$
小球上摆的过程,由机械能守恒定律有:
$\frac{1}{2}$•2mv12=2mgl(1-cosθ),
解得:cosθ=$\frac{2}{3}$,θ=cos-1$\frac{2}{3}$
(1-2)对滑块,由动量定理有 I=0-mv2=2m$\sqrt{\frac{2gl}{3}}$
(1-3)对小球,由动能定理得
-W=2mgl-$\frac{1}{2}$•2mv12,W=-$\frac{4}{3}$mgl
(2)设小球下落到绳与导轨夹角为α时,速度为v,其水平分速度为v1,竖直分速度为v2,此时滑块速度为v3,由水平方向动量守恒得:
2mv1+mv3=0,v3=-2v1
沿绳方向两端速度相等得:v2sinα-v1cosα=v3cosα,
解得:v2=3v1cotα,
再由机械能守恒得:$\frac{1}{2}$mv32+$\frac{1}{2}$•2m(v12+v22)=2mglsinα,
解得:v12=$\frac{2glsi{n}^{3}α}{3si{n}^{2}α+9co{s}^{2}α}$
v2=v12+v22=2glsinα$\frac{si{n}^{2}α+9co{s}^{2}α}{3si{n}^{2}α+9co{s}^{2}α}$
利用图形计算器的函数功能,可以得:α=51.38°,vmax=1.098$\sqrt{gl}$
答:(1-1)小球继续向左摆动达到最高点时,轻绳与竖直方向的夹角是cos-1$\frac{2}{3}$.
(1-2)挡板对滑块的冲量是2m$\sqrt{\frac{2gl}{3}}$.
(1-3)小球从释放到第一次达到最低点的过程中,轻绳拉力对小球做的功是-$\frac{4}{3}$mgl.
(2)将小球由静止释放,若长轨道上无挡板,小球在下落过程中速率的最大值是1.098$\sqrt{gl}$.
点评 本题关键要抓住滑块被挡板粘住前系统的水平方向动量守恒,系统的机械能守恒、滑块被挡板粘住后小球的机械能守恒,滑块与挡板碰撞前后,小球的速度不变.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案 用细绳拴一个质量为m的小球,小球将一固定在墙上的水平轻质弹簧压缩了x(小球与弹簧不拴连),如图所示.将细绳剪断后( )
用细绳拴一个质量为m的小球,小球将一固定在墙上的水平轻质弹簧压缩了x(小球与弹簧不拴连),如图所示.将细绳剪断后( )| A. | 小球立即获得$\frac{kx}{m}$加速度 | |
| B. | 小球在细绳剪断瞬间起开始做平抛运动 | |
| C. | 小球落地的时间等于$\sqrt{\frac{2h}{g}}$ | |
| D. | 小球落地的速度等于$\sqrt{2gh}$ |
 如图所示,由于地球的自转,地球表面上P、Q两点均绕地球自转轴做匀速圆周运动,对于P、Q 两点的运动,下列说法正确的是( )
如图所示,由于地球的自转,地球表面上P、Q两点均绕地球自转轴做匀速圆周运动,对于P、Q 两点的运动,下列说法正确的是( )| A. | P、Q 两点的线速度大小相等 | B. | P、Q两点的角速度大小相等 | ||
| C. | P点的角速度比Q 点的角速度大 | D. | P点的线速度比Q 点的线速度小 |
 5月25日傍晚,一场雨后北京的天空中出现了“双彩虹”的美丽景色.我们所说的“双彩虹”实际上就是虹和霓,虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,我们可利用白光照射玻璃球的实验来模拟说明.现用两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示,M、N、P、Q点的颜色分别为( )
5月25日傍晚,一场雨后北京的天空中出现了“双彩虹”的美丽景色.我们所说的“双彩虹”实际上就是虹和霓,虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,我们可利用白光照射玻璃球的实验来模拟说明.现用两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示,M、N、P、Q点的颜色分别为( )| A. | 紫、红、红、紫 | B. | 红、紫、红、紫 | C. | 红、紫、紫、红 | D. | 紫、红、紫、红 |
| A. | 先有作用力,才有反作用力 | |
| B. | 只有两物体处于平衡状态时,作用力和反作用力才大小相等 | |
| C. | 只有两个物体质量相同时,作用力和反作用力才大小相等 | |
| D. | 以上说法都不正确 |
| A. | 垂直磁子午线由西向东 | B. | 垂直磁子午线由东向西 | ||
| C. | 沿磁子午线由南向北 | D. | 沿磁子午线由北向南 |
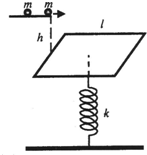 如图所示,质量为m,边长为l的正方形平板与弹簧相连,弹簧的劲度系数为k,另一端固定于地面,平板处于平衡状态.质量为m的第一个小球从平台以一定速度垂直于平板的左边缘水平抛出,并与平板发生完全非弹性碰撞(设平台与板间高度差为h,抛出点在平板的左边缘正上方).隔一段时间后,以相同速度抛出第二个小球.(假定在任何情况下平板始终保持水平,忽略平板在水平方向上的运动,且为方便计算起见,设h=3$\frac{mg}{k}$)
如图所示,质量为m,边长为l的正方形平板与弹簧相连,弹簧的劲度系数为k,另一端固定于地面,平板处于平衡状态.质量为m的第一个小球从平台以一定速度垂直于平板的左边缘水平抛出,并与平板发生完全非弹性碰撞(设平台与板间高度差为h,抛出点在平板的左边缘正上方).隔一段时间后,以相同速度抛出第二个小球.(假定在任何情况下平板始终保持水平,忽略平板在水平方向上的运动,且为方便计算起见,设h=3$\frac{mg}{k}$)