题目内容
2.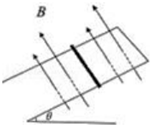 如图所示,有一光滑、不计电阻且较长的“Ⅱ”平行金属导轨,间距L=1m,导轨所在的平面与水平面的倾角为37°,导轨空间内存在垂直导轨平面的匀强磁场.现将一质量m=0.1kg、电阻R=2Ω的金属杆水平靠在导轨处,与导轨接触良好.(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,有一光滑、不计电阻且较长的“Ⅱ”平行金属导轨,间距L=1m,导轨所在的平面与水平面的倾角为37°,导轨空间内存在垂直导轨平面的匀强磁场.现将一质量m=0.1kg、电阻R=2Ω的金属杆水平靠在导轨处,与导轨接触良好.(g=10m/s2,sin37°=0.6,cos37°=0.8)(1)若磁感应强度随时间变化满足B=2+0.2t(T),金属杆由距导轨顶部l m处释放,求至少经过多长时间释放,会获得沿斜面向上的加速度;
(2)若匀强磁场大小为定值,对金属杆施加一个平行于导轨斜面向下的外力F,其大小为产F=v+0.4(N),v为金属杆运动的速度,使金属杆以恒定的加速度a=10m/s2沿导轨向下做匀加速运动,求匀强磁场磁感应强度B的大小;
(3)若磁感应强度随时间变化满足B=$\frac{2}{0.1+0.1{t}^{2}}$(T),t=0时刻金属杆从离导轨顶端S0=1m处静止释放,同时对金属杆施加一个外力,使金属杆沿导轨下滑且没有感应电流产生,求金属杆下滑5m所用的时间.
分析 (1)金属杆有沿着斜面向上的加速度时,安培力等于重力沿斜面的分力,由安培力表达式F=BIL,结合B随t的变化关系,可以解得时间t;
(2)金属杆收到重力和安培力的作用而做匀加速运动,由牛顿第二定律,结合安培力表达式,可解得磁感应强度B.
(3)金属杆沿导轨下滑且没有感应电流产生,说明磁通量不变,由此可以表示初末磁通量相等,解得金属杆下滑5m所用的时间.
解答 解:(1)设金属杆长为L,距离导轨顶部也为L,经过ts后,金属杆有沿斜面向上的加速度,此时安培力等于重力沿斜面的分力,则:
${F}_{A}^{\;}=mgsinθ$
又:${F}_{A}^{\;}=BIL=B\frac{E}{R}L$
其中:$E=\frac{△B}{△t}{L}_{\;}^{2}=0.2V$
所以:$(2+0.2t)\frac{E}{R}L=mgsinθ$
解得:t=20s
(2)对金属杆由牛顿第二定律:
$mgsinθ+F-{F}_{A}^{\;}=ma$
代入数据解得:$1+(1-\frac{{B}_{\;}^{2}}{2})v=0.1×10$
因为是匀加速运动,加速度为定值,则:$(1-\frac{{B}_{\;}^{2}}{2})=0$
解得:$B=\sqrt{2}T$
(3)设t=0时刻金属杆距离顶端为${S}_{0}^{\;}$,由金属杆与导轨组成的闭合电路中,磁通量保持不变,经过ts的位移为S,则:
${B}_{1}^{\;}L{S}_{0}^{\;}={B}_{2}^{\;}L(S+{S}_{0}^{\;})$
代入数据:
$20×1×1=\frac{2}{0.1+0.1{t}_{\;}^{2}}×1×(1+S)$
解得:$S={t}_{\;}^{2}$
金属杆做初速度为零的匀加速直线运动,S=5m
解得:$t=\sqrt{5}s$
答:(1)若磁感应强度随时间变化满足B=2+0.2t(T),金属杆由距导轨顶部l m处释放,至少经过20s时间释放,会获得沿斜面向上的加速度;
(2)若匀强磁场大小为定值,对金属杆施加一个平行于导轨斜面向下的外力F,其大小为产F=v+0.4(N),v为金属杆运动的速度,使金属杆以恒定的加速度a=10m/s2沿导轨向下做匀加速运动,匀强磁场磁感应强度B的大小为$\sqrt{2}T$;
(3)若磁感应强度随时间变化满足B=$\frac{2}{0.1+0.1{t}^{2}}$(T),t=0时刻金属杆从离导轨顶端S0=1m处静止释放,同时对金属杆施加一个外力,使金属杆沿导轨下滑且没有感应电流产生,金属杆下滑5m所用的时间$\sqrt{5}s$.
点评 该题的关键是第三问,要能正确解读“金属杆沿导轨下滑且没有感应电流产生的含义,只有这样才能顺利解决该题,其余方法均不行

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | 电吹风 | B. | 金属探测仪 | C. | 电饭煲 | D. | 电话机 |
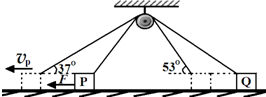 如图所示,重物P、Q由刚性绳拴接,跨过定滑轮处于图中实际位置,此时绳恰好拉紧,重物静止在水平面上,用外力水平向左拉P至虚线位置,已知sin37°=0.6,sin53°=0.8,当P的水平速度为15m/s时,Q的速度为( )
如图所示,重物P、Q由刚性绳拴接,跨过定滑轮处于图中实际位置,此时绳恰好拉紧,重物静止在水平面上,用外力水平向左拉P至虚线位置,已知sin37°=0.6,sin53°=0.8,当P的水平速度为15m/s时,Q的速度为( )| A. | 10m/s | B. | 12m/s | C. | 15m/s | D. | 20m/s |
| A. | 开普勒经过多年的研究发现了万有引力定律 | |
| B. | 牛顿通过计算首先发现了海王星和冥王星 | |
| C. | 英国物理学家卡文迪许用实验的方法测出引力常量G | |
| D. | 库仑最早引入了电场概念,并提出用电场线表示电场 |
| A. | 奥斯特发现了电流磁效应;法拉第发现了电磁感应 | |
| B. | 麦克斯韦预言了电磁波的存在;楞次用实验证实了电磁波的存在 | |
| C. | 库仑发现了点电荷的相互作用规律;赫兹通过油滴实验测定了元电荷的数值 | |
| D. | 杨氏双缝干涉实验证明光具有波动性;光的衍射证明光是横波 |
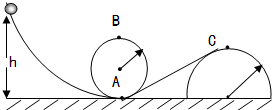 如图所示,两光滑圆轨道的半径R1=25cm,R2=50cm.质量为250g的小球从h=70cm高处无摩擦地滚下.求:
如图所示,两光滑圆轨道的半径R1=25cm,R2=50cm.质量为250g的小球从h=70cm高处无摩擦地滚下.求: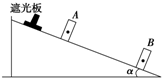 某实验小组利用光电计时器探究物块沿倾斜气垫导轨下滑过程中重力做功与动能的关系,装置如图甲所示,让小物块从倾斜气垫导轨顶端滑下.若测得小物块通过A、B光电门的时间分别为t1和t2,A、B之间的距离为L,遮光板的宽度为d,斜面的倾角为α,重力加速度为g.
某实验小组利用光电计时器探究物块沿倾斜气垫导轨下滑过程中重力做功与动能的关系,装置如图甲所示,让小物块从倾斜气垫导轨顶端滑下.若测得小物块通过A、B光电门的时间分别为t1和t2,A、B之间的距离为L,遮光板的宽度为d,斜面的倾角为α,重力加速度为g. (1)在《探究求合力的方法》的实验中,其中的二个步骤是:
(1)在《探究求合力的方法》的实验中,其中的二个步骤是: