题目内容
16.某实验小组利用图(a)所示实验装置及数字化信息系统探究“外力做功与小车动能变化的关系”.实验时将小车拉到水平轨道的O位置由静止释放,在小车从O位置运动到 A位置过程中,经计算机处理得到了弹簧弹力与小车位移的关系图线如图(b)所示,还得到了小车在 A位置的速度大小vA;另外用电子秤测得小车(含位移传感器发射器)的总质量为m.回答下列问题:
(1)由图(b)可知,图(a)中A位置到力传感器的距离大于(“小于”、“等于”或“大于”)弹簧原长.
(2)小车从O位置运动到A位置过程中弹簧对小车所做的功W=$\frac{{F}_{0}+{F}_{A}}{2}$•xA,小车的动能改变量△Ek=$\frac{1}{2}$m${v}_{A}^{2}$.(用m、vA、FA、F0、xA中各相关物理量表示)
(3)若将弹簧从小车上卸下,给小车一初速度v0,让小车从轨道右端向左端滑动,利用位移传感器和计算机得到小车的速度随时间变化的图线如图(c)所示,则小车所受轨道摩擦力的大小f=m$\frac{{v}_{0}}{{t}_{m}}$.( 用m、v0、tm中各相关物理量表示)
(4)综合步骤(2)、(3),该实验所要探究的“外力做功与小车动能变化的关系”表达式是(F0+FA-2m$\frac{{v}_{0}}{{t}_{m}}$)xA=mvA2.(用m、vA、FA、F0、xA、v0、tm中各相关物理量表示)
分析 (1)根据计算机处理得到了弹簧弹力与小车位移的关系图线与胡克定律分析答题.
(2)根据功的定义,结合F-t图即可求出拉力的功;根据动能的定义式,结合图象即可求出动能的变化.
(3)由公式:W总=W-fSA和f=ma=m$\frac{{v}_{0}}{{t}_{m}}$,结合图象c即可求出;
(4)结合平衡摩擦力的方法判断即可.
解答 解:(1)根据计算机处理得到了弹簧弹力与小车位移的关系图线可知,弹簧的弹力随弹簧长度的减小而减小,可知弹簧的长度减小时,伸长量减小,A位置弹簧仍然处于伸长状态,因此力传感器的距离大于弹簧原长;
(2)根据功的定义可知,功是力在空间的积累效果,W=FS,
结合F-S图象可知,小车从O到A的过程中,拉力做的功可以用梯形的面积来表示,即:W=$\frac{{F}_{0}+{F}_{A}}{2}$•xA,
小车的初速度是0,末速度是vA,则动能的改变量:△Ek=$\frac{1}{2}$m${v}_{A}^{2}$-0=$\frac{1}{2}$m${v}_{A}^{2}$
(3)根据图c可知,小车在不受弹簧的弹力时做匀减速直线运动,说明小车受到摩擦力的作用,
结合图c可知,小车的加速度:a=$\frac{△v}{△t}$=$\frac{{v}_{0}}{{t}_{m}}$,所以,小车受到的摩擦力:f=ma=m$\frac{{v}_{0}}{{t}_{m}}$
由此可知,在有弹簧的弹力时,弹簧的弹力和摩擦力共同为小车做功,则:W总=W-fSA
(4)由(3)的分析可知,小车运动的过程中,该同学需要验证的关系式是:(F0+FA-2m$\frac{{v}_{0}}{{t}_{m}}$)xA=mvA2;
故答案为:(1)大于;(2)$\frac{{F}_{0}+{F}_{A}}{2}$•xA,$\frac{1}{2}$m${v}_{A}^{2}$;(3)m$\frac{{v}_{0}}{{t}_{m}}$; (4):(F0+FA-2m$\frac{{v}_{0}}{{t}_{m}}$)xA=mvA2.
点评 通过作出两个量的图象,然后由图象去寻求未知量与已知量的关系.运用数学知识和物理量之间关系式结合起来求解.

| A. | 冬天,在结冰的公路上洒上沙子可以防滑 | |
| B. | 电磁灶可以加热砂锅里的食物 | |
| C. | 加油站工作人员穿化纤服装,是为了防止静电 | |
| D. | 一个额定功率200瓦的家用电冰箱,一天24小时的耗电量4.8千瓦时 |
 在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )
在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )| A. | 无感应电流 | |
| B. | 感应电流逐渐变大 | |
| C. | 感应电流为顺时针方向,大小为$\frac{{{L^2}{B_0}}}{{{t_0}R}}$ | |
| D. | 感应电流为逆时针方向,大小为$\frac{{2{L^2}{B_0}}}{{{t_0}R}}$ |
| A. | β衰变现象说明电子是原子核的组成部分 | |
| B. | 目前已建成的核电站的能量来自于重核裂变 | |
| C. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能增大,原子总能量增大 | |
| D. | 卢瑟福依据极少数α粒子发生大角度散射提出了原子核式结构模型 |
 在输液时,药液有时会从针口流出体外,为了及时发现,某人设计了一种自动报警装置,电路如图所示.定值电阻R、探测器S电阻均保持不变.M是贴在针口处的传感器,当接触到药液时其电阻RM会发生明显变化,导致S两端电压U增大,装置发出警报,此时( )
在输液时,药液有时会从针口流出体外,为了及时发现,某人设计了一种自动报警装置,电路如图所示.定值电阻R、探测器S电阻均保持不变.M是贴在针口处的传感器,当接触到药液时其电阻RM会发生明显变化,导致S两端电压U增大,装置发出警报,此时( )| A. | RM变大,且R越大,探测器S越灵敏 | B. | RM变大,且R越小,探测器S越灵敏 | ||
| C. | RM变小,且R越大,探测器S越灵敏 | D. | RM变小,且R越小,探测器S越灵敏 |
| A. | 简谐运动的周期与振幅无关 | |
| B. | 在弹簧振子做简谐运动的回复力表达式F=-kx中,F为振动物体受到的合外力,k为弹簧的劲度系数 | |
| C. | 在波传播方向上,某个质点的振动速度就是波的传播速度 | |
| D. | 在双缝干涉实验中,同种条件下用紫光做实验比红光做实验得到的条纹更宽 |
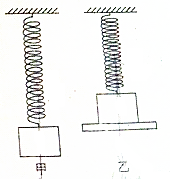 如图甲所示,一质量不计的劲度系数为k的轻弹簧上端固定,下端悬吊一质量为m的物块,现用一质量为M的托盘向上压缩弹簧,如图乙所示,当托盘突然撤走时物块具有向下的加速度,其大小为a(a>g).如果用一外力作用在托盘上,使托盘和物块共同向下以$\frac{a}{3}$的加速度做匀加速直线运动.求:
如图甲所示,一质量不计的劲度系数为k的轻弹簧上端固定,下端悬吊一质量为m的物块,现用一质量为M的托盘向上压缩弹簧,如图乙所示,当托盘突然撤走时物块具有向下的加速度,其大小为a(a>g).如果用一外力作用在托盘上,使托盘和物块共同向下以$\frac{a}{3}$的加速度做匀加速直线运动.求: 如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求:
如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求: 如图所示,水平传送带PQ间相距L1=1.2m,传送带以v0=2m/s的速度顺时针匀速运动,传送带处在与水平方向成α=37°斜向上的匀强电场中,电场强度E=1×103V/m,倾角θ=30°斜面底端固定一轻弹簧,轻弹簧处于原长时上端位于C点,Q点与斜面平滑连接,Q到C点的距离L2=1.4m.现有质量m=1kg,电量q=1×10-2C的物体(可视为质点)无初速地轻放在传送带左端的P点,物体被传送到右端Q点后沿斜面向下滑动,将弹簧压缩到最短位置D点后恰能弹回C点.不计物体经过Q点时机械能的损失,整个过程中物体的电量保持不变,已知物体与传送带、斜面间的动摩擦因数分别为μ1=0.5、μ2=$\frac{\sqrt{3}}{2}$.(g取10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,水平传送带PQ间相距L1=1.2m,传送带以v0=2m/s的速度顺时针匀速运动,传送带处在与水平方向成α=37°斜向上的匀强电场中,电场强度E=1×103V/m,倾角θ=30°斜面底端固定一轻弹簧,轻弹簧处于原长时上端位于C点,Q点与斜面平滑连接,Q到C点的距离L2=1.4m.现有质量m=1kg,电量q=1×10-2C的物体(可视为质点)无初速地轻放在传送带左端的P点,物体被传送到右端Q点后沿斜面向下滑动,将弹簧压缩到最短位置D点后恰能弹回C点.不计物体经过Q点时机械能的损失,整个过程中物体的电量保持不变,已知物体与传送带、斜面间的动摩擦因数分别为μ1=0.5、μ2=$\frac{\sqrt{3}}{2}$.(g取10m/s2,sin37°=0.6,cos37°=0.8).求: