题目内容
12. 如图所示.在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨.导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一报金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.己知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.求:
如图所示.在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨.导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一报金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.己知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.求:(1)金属棒从M点被抛出至落回M点的整个过程中,电阻R消耗的电能;
(2)当金属棒向下运动达到稳定状态时的速度大小v;
(3)经典物理学认为,金属的电阻源于定向运动的自由电子与金属离子的碰撞.已知元电荷为e,求当金属棒向下运动达到稳定状态时,棒中金属离子对一个自由电子沿棒方向的平均作用力大小.
分析 (1)金属棒从M点被抛出至落回M点的整个过程中,动能减少转化为电能,根据能量守恒定律求电阻R消耗的电能.
(2)当金属棒向下运动达到稳定状态时重力的功率等于回路的电功率.由此列式求解最大速度.
(3)根据电流的微观表达式I=neSv和金属棒生热功率公式Pr=(nSL)fv,结合进行解答.
解答 解:(1)金属棒从M点被抛出至落回M点的整个过程中,由能量守恒得
回路中消耗的电能 Q=$\frac{1}{2}$mv02-$\frac{1}{2}$m($\frac{{v}_{0}}{2}$)2=$\frac{3}{8}$mv02,
电阻R消耗的电能 QR=$\frac{R}{R+r}$Q=$\frac{3mR{v}_{0}^{2}}{8(R+r)}$.
(2)当金属棒向下运动达到稳定状态时作匀速直线运动,
设最大速度为v,则有 mgv=$\frac{{E}^{2}}{R+r}$,其中 E=BLv,解得:v=$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$;
(3)当金属棒向下运动达到稳定状态时
单位时间内机械能减少 P=mgvm,
金属棒生热功率:Pr=$\frac{r}{R+r}$P,
回路中的电流:I=$\frac{BLv}{R+r}$,
设棒的横截面积为S,棒中单位体积内的自由电子数为n,
棒中自由电子定向移动的速度为v,金属离子对自由电子的平均作用力为f.
则 Pr=(nSL)fv,I=neSv.所以:f=$\frac{emgr}{B{L}^{2}}$;
答:(1)金属棒从M点被抛出至落回M点的整个过程中,a.电阻R消耗的电能为$\frac{3mR{v}_{0}^{2}}{8(R+r)}$.
(2)当金属棒向下运动达到稳定状态时,所具有的最大速度为$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$.
(3)棒中金属离子对一个自由电子沿棒方向的平均作用力大小为$\frac{emgr}{B{L}^{2}}$.
点评 本题是一道电磁感应与力学相结合的综合题,解决本题的是握金属棒稳定的条件,理解宏观与微观联系的桥梁是电流的微观表达式.

 阅读快车系列答案
阅读快车系列答案 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线栓在竖直挡板上,球与挡板间有一根被压缩的轻质弹簧,当烧断细线时,小球被弹出,小球离开平台前弹簧已恢复原长,已知小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线栓在竖直挡板上,球与挡板间有一根被压缩的轻质弹簧,当烧断细线时,小球被弹出,小球离开平台前弹簧已恢复原长,已知小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10m/s2)( )| A. | 25J | B. | 20J | C. | 15J | D. | 10J |
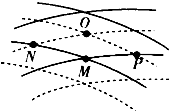 如图所示,实线与虚线分别表示振幅(振幅为A)、频率均相同的两列波的波峰和波谷.此刻M是波峰与波峰的相遇点,下列说法中不正确的是( )
如图所示,实线与虚线分别表示振幅(振幅为A)、频率均相同的两列波的波峰和波谷.此刻M是波峰与波峰的相遇点,下列说法中不正确的是( )| A. | 0、M连线的中点是振动加强的点,其振幅为2A | |
| B. | P、N两处的质点始终处在平衡位置 | |
| C. | 随着时间的推移,M处的质点将向O处移动 | |
| D. | 从该时刻起,经过四分之一周期,M处的质点到达平衡位置,此时位移为零 |
| A. | 125m/s,与v0反向 | B. | 90m/s,与v0反向 | C. | 240m/s,与v0反向 | D. | 以上答案都错 |
 簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.关于小球下降阶段,下列说法中正确的是( )
簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.关于小球下降阶段,下列说法中正确的是( )| A. | 运动到B点的速度最大 | |
| B. | B点运动到D点期间小球动能先增大后减小 | |
| C. | 运动到C点小球动能最小 | |
| D. | B点到D点小球的减小动能等于增加的弹性势能 |
 某探究学习小组的同学试图以图中的滑块为对象验证“动能定理”,他们在实验室组装了如图所示的一套装置,另外他们还找到了打点计时器所用的学生电源、导线、复写纸、小木块、细沙.当连上纸带,释放沙桶时,滑块处于静止.要完成该实验,你认为:
某探究学习小组的同学试图以图中的滑块为对象验证“动能定理”,他们在实验室组装了如图所示的一套装置,另外他们还找到了打点计时器所用的学生电源、导线、复写纸、小木块、细沙.当连上纸带,释放沙桶时,滑块处于静止.要完成该实验,你认为: 如图所示,质量为m1=3kg的小物块A置于水平面上,A与水平面间的动摩擦因数为μ=0.2,质量为m2=1kg的小物块B用不可伸长的细线悬挂着,细线的另一端系在O点,细线长l=0.5m,处于伸直状态且竖直,A、B可视为质点,它们的水平距离s=2.25m,现A以水平初速度v0=5m/s向右滑动并与B发生弹性正撞,取g=10m/s2,求:
如图所示,质量为m1=3kg的小物块A置于水平面上,A与水平面间的动摩擦因数为μ=0.2,质量为m2=1kg的小物块B用不可伸长的细线悬挂着,细线的另一端系在O点,细线长l=0.5m,处于伸直状态且竖直,A、B可视为质点,它们的水平距离s=2.25m,现A以水平初速度v0=5m/s向右滑动并与B发生弹性正撞,取g=10m/s2,求: