题目内容
13.某星球质量为M,半径为R,可视为质量分布均匀的球体,一人在该星球表面上距星球表面高为h(h远小于R)处以初速度V0水平抛出一个质量为m的小球,不计任何阻力,万有引力常量为G,求:(1)抛球过程中人对小球所做的功W
(2)星球表面的重力加速度g的大小
(3)小球落到星球表面时的速度V的大小.
分析 (1)由动能定理可以求出人做的功.
(2)根据万有引力等于重力可以求出重力加速度.
(3)应用动能定理可以求出落地速度.
解答 解:(1)对小球,由动能定理得:W=$\frac{1}{2}$mv02;
(2)在星球表面的物体:G$\frac{Mm}{{R}^{2}}$=mg,解得:g=$\frac{GM}{{R}^{2}}$;
(3)对物体,由动能定理得:mgh=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02,
解得:v=$\sqrt{{v}_{0}^{2}+\frac{2GMh}{{R}^{2}}}$;
答:(1)抛球过程中人对小球所做的功W为$\frac{1}{2}$mv02;
(2)星球表面的重力加速度g的大小为$\frac{GM}{{R}^{2}}$;
(3)小球落到星球表面时的速度V的大小为$\sqrt{{v}_{0}^{2}+\frac{2GMh}{{R}^{2}}}$.
点评 本题考查了求功、重力加速度、速度问题,分析清楚小球的运动过程,应用动能定理、万有引力公式与牛顿第二定律可以解题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
3.如图所示的电路中,L1和L2是完全相同的灯泡,线圈L的电阻可以忽略,下列说法中正确的是( )


| A. | 合上开关S接通电路后,L2始终比L1亮 | |
| B. | 合上开关S接通电路后,L1先亮,L2缓慢变亮,最后一样亮 | |
| C. | 断开开关S切断电路后,L2先熄灭,L1过一会儿才熄灭 | |
| D. | 断开开关S切断电路后,L1和L2都过一会儿才熄灭 |
4.在下列情况中,画横线的物体可以看作质点的是( )
| A. | 研究从成都开津上海的一列火车的运行时间 | |
| B. | 观察正在做课间操的小徐同学动作是否到位 | |
| C. | 研究“神州八号”和“天宫一号”如何对接 | |
| D. | 观察舰载飞机起飞时的航空母舰 |
1. 两轮自平衡电动车具有运动灵活、智能控制、操作简单、绿色环保、转弯半径为零等优点,如图所示,警察正脚踏自平衡电动车巡逻.下列分析正确的是( )
两轮自平衡电动车具有运动灵活、智能控制、操作简单、绿色环保、转弯半径为零等优点,如图所示,警察正脚踏自平衡电动车巡逻.下列分析正确的是( )
 两轮自平衡电动车具有运动灵活、智能控制、操作简单、绿色环保、转弯半径为零等优点,如图所示,警察正脚踏自平衡电动车巡逻.下列分析正确的是( )
两轮自平衡电动车具有运动灵活、智能控制、操作简单、绿色环保、转弯半径为零等优点,如图所示,警察正脚踏自平衡电动车巡逻.下列分析正确的是( )| A. | 自平衡电动车及人受到的重力和对地面的压力是一对平衡力 | |
| B. | 自平衡电动车及人受到的重力和地面对他们的支持力是一对相互作用力 | |
| C. | 轮胎上凹凸不平的花纹是为了增加车对地面的压力 | |
| D. | 自平衡电动车运动灵活是因为惯性比较小 |
18. 如图所示,A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的形变弹性限度内,则( )
如图所示,A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的形变弹性限度内,则( )
 如图所示,A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的形变弹性限度内,则( )
如图所示,A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的形变弹性限度内,则( )| A. | 保持+Q不变,将+q变为一q,平衡时弹簧的缩短量等于x0 | |
| B. | 保持+q不变,将+Q变为一Q,平衡时弹簧的缩短量小于x0 | |
| C. | 保持+Q不变,将+q变为+2q,平衡时弹簧的伸长量等于2x0 | |
| D. | 保持+q不变,将+Q变为+2Q,平衡时弹簧的伸长量小于2x0 |
2. 如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )
如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )
 如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )
如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )| A. | A球的速率小于B球的速率 | |
| B. | A球的角速度大于B球的角速度 | |
| C. | A球的转动周期大于B球的转动周期 | |
| D. | A球对漏斗壁的压力大于B球对漏斗壁的压力 |
3.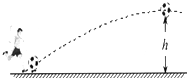 如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )
如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )
 如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )
如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )| A. | 运动员踢球时对足球做功$\frac{1}{2}$mv2 | |
| B. | 运动员踢球时对足球做功mgh+$\frac{1}{2}$mv2 | |
| C. | 足球上升过程克服重力做功mgh+$\frac{1}{2}$mv2 | |
| D. | 足球上升过程克服重力做功mgh |
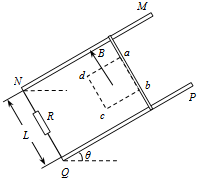 如图所示,间距为L,足够长的光滑金属导轨MN和PQ放在倾角为θ的斜面上,在N和Q之间连有一个阻值为R电阻.两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向垂直斜面向上的匀强磁场,磁感应强度为B.在导轨上放置一根与导轨垂直的金属杆,金属杆质量为m、电阻为r.金属杆从ab处无初速释放,运动过程中始终与导轨保持垂直且接触良好,金属杆离开磁场前已做匀速运动,不计导轨的电阻,重力加速度为g.求:
如图所示,间距为L,足够长的光滑金属导轨MN和PQ放在倾角为θ的斜面上,在N和Q之间连有一个阻值为R电阻.两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向垂直斜面向上的匀强磁场,磁感应强度为B.在导轨上放置一根与导轨垂直的金属杆,金属杆质量为m、电阻为r.金属杆从ab处无初速释放,运动过程中始终与导轨保持垂直且接触良好,金属杆离开磁场前已做匀速运动,不计导轨的电阻,重力加速度为g.求:


