题目内容
12. 如图,一粒子发射源P位于足够大绝缘板AB的上方d处,能够在纸面内向各个方向发射速率为v、电荷量为q质量为m的带正电的粒子,空间存在垂直纸面的匀强磁场,不考虑粒子间的相互作用和粒子重力.已知粒子做圆周运动的半径大小恰好为d,则( )
如图,一粒子发射源P位于足够大绝缘板AB的上方d处,能够在纸面内向各个方向发射速率为v、电荷量为q质量为m的带正电的粒子,空间存在垂直纸面的匀强磁场,不考虑粒子间的相互作用和粒子重力.已知粒子做圆周运动的半径大小恰好为d,则( )| A. | 能打在板上的区域长度是2d | |
| B. | 能打在板上的区域长度是($\sqrt{3}$+1)d | |
| C. | 同一时刻发射出的带电粒子达到板上的最大时间差为$\frac{7πd}{6v}$ | |
| D. | 同一时刻发射出的带电粒子达到板上的最大时间差为$\frac{πqd}{6mv}$ |
分析 作出粒子在磁场中运动轨迹的临界状态,结合半径公式,通过几何关系求出带电粒子能到达板上的长度;作出粒子在磁场中运动时间最长和最短粒子运动轨迹,结合几何关系得出最大时间差.
解答 解:A、B、打在极板上粒子轨迹的临界状态如图所示:
根据几何关系知,带电粒子能到达板上的长度l=R+$\sqrt{3}$R=(1+$\sqrt{3}$)R=(1+$\sqrt{3}$)d;故A错误,B正确;
C、D、在磁场中运动时间最长和最短粒子运动轨迹示意图如图所示:
由几何关系知,最长时间t1=$\frac{3}{4}$T
最短时间t2=$\frac{1}{6}$T
又有粒子在磁场中运动的周期T=$\frac{2πr}{v}$=$\frac{2πd}{v}$;
根据题意:t1-t2=△t
联立解得:△t=$\frac{7}{12}T$=$\frac{7πd}{6v}$;故C正确,D错误;
故选:BC.
点评 本题考查了带电粒子在匀强磁场中的运动,带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力;确定带电粒子轨迹的范围一般应用画图的方法找出,同时可以结合几何知识进行分析.

练习册系列答案
相关题目
2. 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )| A. | 电流表的示数为4.4A | |
| B. | 原线圈的输入功率为16W | |
| C. | 电压表的示数为20V | |
| D. | 通过电阻R的交变电流的频率为100Hz |
20.一列简谐横波沿x轴传播,图甲是波刚好传播到x=5m处的M点的波形图,图乙是质点N(x=3m)从此时刻开始计时的振动图象,Q是位于x=9m处的质点.下列说法正确的是 ( )


| A. | 这列波的波长是4m | |
| B. | 这列波的传播速度是1.25m/s | |
| C. | M点以后的各质点开始振动时的方向都沿y轴正方向 | |
| D. | 质点Q经过7s时,第一次到达波峰 |
7.物理学中,科学家处理物理问题用到了多种思想与方法,根据你对物理学的学习,关于科学家的思想和贡献,下列说法正确的是( )
| A. | 伽利略猜想做自由落体运动的物体,其下落的距离与时间成正比,并用实验进行了验证 | |
| B. | 牛顿首先提出“提出假说,数学推理,实验验证,合理外推”的科学推理方法 | |
| C. | 赫兹首次用实验证实了电磁波的存在 | |
| D. | 麦克斯韦提出了狭义相对论 |
17. 如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )
如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )
 如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )
如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )| A. | 方向与水平方向的夹角为30°,大小为2v | |
| B. | 方向与水平方向的夹角为60°,大小为2v | |
| C. | 方向与水平方向的夹角为30°,大小为$\sqrt{3}$v | |
| D. | 方向与水平方向的夹角为60°,大小为$\sqrt{3}$v |
4.若规定向正东为位移的正方向,今有一个皮球停在水平面的某处,轻踢它一脚,使它向正东做直线运动,运动5m远与墙相碰,后又向正西做直线运动,运动7m后停下.则上述过程中皮球通过的路程和位移分别是( )
| A. | 12m、2m | B. | 12m、-2m | C. | -2m、2m | D. | 2m、-2m |
1. 2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
 2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
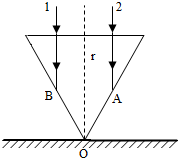 在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则:
在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则: 如图所示,是探究向心力的大小F与质量m、角速度ω和半径r之间的关系的实验装置图,转动手柄1,可使变速轮塔2和3以及长槽4和短槽5随之匀速转动.皮带分别套在轮塔2和3上的不同圆盘上,可使两个槽内的小球6、7分别以不同的角速度做匀速圆周运动.小球做圆周运动的向心力由横臂8的挡板对小球的压力提供,球对挡板的反作用力,通过横臂8的杠杆作用使弹簧测力筒9下降,从而露出标尺10,标尺10上露出的红白相间的等分格显示出两个球所受向心力的比值.那么:
如图所示,是探究向心力的大小F与质量m、角速度ω和半径r之间的关系的实验装置图,转动手柄1,可使变速轮塔2和3以及长槽4和短槽5随之匀速转动.皮带分别套在轮塔2和3上的不同圆盘上,可使两个槽内的小球6、7分别以不同的角速度做匀速圆周运动.小球做圆周运动的向心力由横臂8的挡板对小球的压力提供,球对挡板的反作用力,通过横臂8的杠杆作用使弹簧测力筒9下降,从而露出标尺10,标尺10上露出的红白相间的等分格显示出两个球所受向心力的比值.那么: