题目内容
9.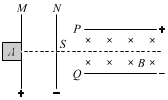 带电粒子的电荷量与质量的比值称为比荷,是描述带电粒子的重要参数.如图所示是某种测量带电粒子比荷实验的原理示意图,一对平行金属板M、N竖直放置,板间存在水平方向的匀强电场;另一对平行金属板P、Q水平放置,两板间距为d,板间存在竖直方向的匀强电场和垂直纸面向里的匀强磁场.在某次实验中,粒子源A不断产生某种带正电的粒子,带电粒子经金属板M、N间的电场加速,从N板上的小孔S射出,沿水平方向进入金属板P、Q间.调节电场和磁场,当M、N两板间的电势差为U1,P、Q两板间的电势差为U2,磁感应强度为B时,带电粒子在P、Q两板间恰好做匀速直线运动.粒子运动轨迹如图中虚线所示.设带电粒子离开粒子源时的速度、所受重力及粒子间的相互作用均可忽略.
带电粒子的电荷量与质量的比值称为比荷,是描述带电粒子的重要参数.如图所示是某种测量带电粒子比荷实验的原理示意图,一对平行金属板M、N竖直放置,板间存在水平方向的匀强电场;另一对平行金属板P、Q水平放置,两板间距为d,板间存在竖直方向的匀强电场和垂直纸面向里的匀强磁场.在某次实验中,粒子源A不断产生某种带正电的粒子,带电粒子经金属板M、N间的电场加速,从N板上的小孔S射出,沿水平方向进入金属板P、Q间.调节电场和磁场,当M、N两板间的电势差为U1,P、Q两板间的电势差为U2,磁感应强度为B时,带电粒子在P、Q两板间恰好做匀速直线运动.粒子运动轨迹如图中虚线所示.设带电粒子离开粒子源时的速度、所受重力及粒子间的相互作用均可忽略.(1)求带电粒子在金属板P、Q间做匀速直线运动时的速度大小v;
(2)求带电粒子的比荷$\frac{q}{m}$;
(3)如果在实验过程中发现带电粒子偏向金属板P,应如何调节电场和磁场,才能使带电粒子在金属板P、Q间做匀速直线运动.请你写出至少两项可行的措施.
分析 (1)粒子做匀速运动,受电场力和洛伦兹力平衡,根据平衡条件即可确定粒子的速度;
(2)根据MN间的加速过程进行分析,根据动能定理即可求得比荷;
(3)分析洛伦兹力和电场力的方向,根据平衡关系即可明确应采取的措施.
解答 解:
(1)金属板P、Q间匀强电场的场强大小$E=\frac{U_2}{d}$
设带电粒子电荷量为q,因为该粒子在金属板P、Q间做匀速直线运动,所以qE=qvB
解得 $v=\frac{U_2}{Bd}$
(2)设带电粒子质量为m,带电粒子在金属板M、N间被加速,根据动能定理$q{U_1}=\frac{1}{2}m{v^2}-0$
解得 $\frac{q}{m}=\frac{U_2^2}{{2{U_1}{B^2}{d^2}}}$
(3)带电粒子偏向金属板P,说明粒子受到的洛伦兹力偏大,故可以采用的措施有:
①增大P、Q两板间的电势差,保持其它条件不变.
②减小P、Q两板间的磁感应强度,保持其它条件不变.
③减小M、N两板间的电势差,保持其它条件不变.
答:(1)带电粒子在金属板P、Q间做匀速直线运动时的速度大小v为$\frac{{U}_{2}}{Bd}$
(2)求带电粒子的比荷$\frac{q}{m}$为$\frac{{U}_{2}^{2}}{2{U}_{1}{B}^{2}{d}^{2}}$;
(3)可行的措施有:①增大P、Q两板间的电势差,保持其它条件不变.
②减小P、Q两板间的磁感应强度,保持其它条件不变.
③减小M、N两板间的电势差,保持其它条件不变.
点评 本题考查带电粒子在电磁场中的运动规律,要注意明确电场和磁场的特点,能正确分析物理过程,从而正确应用动能定理和平衡条件进行分析求解.

练习册系列答案
相关题目
20. 如图所示是一个自制简易电动机原理图,一枚干电池竖直放置(正极朝上),电池的负极上吸有一块圆形的可以导电的小磁体,磁场分布已知,将一个小金属线圈套在电池上,线圈和电池构成闭合回路,通电线圈在磁场的作用下就会转动起来,从上向下附视,线圈的转动方向是( )
如图所示是一个自制简易电动机原理图,一枚干电池竖直放置(正极朝上),电池的负极上吸有一块圆形的可以导电的小磁体,磁场分布已知,将一个小金属线圈套在电池上,线圈和电池构成闭合回路,通电线圈在磁场的作用下就会转动起来,从上向下附视,线圈的转动方向是( )
 如图所示是一个自制简易电动机原理图,一枚干电池竖直放置(正极朝上),电池的负极上吸有一块圆形的可以导电的小磁体,磁场分布已知,将一个小金属线圈套在电池上,线圈和电池构成闭合回路,通电线圈在磁场的作用下就会转动起来,从上向下附视,线圈的转动方向是( )
如图所示是一个自制简易电动机原理图,一枚干电池竖直放置(正极朝上),电池的负极上吸有一块圆形的可以导电的小磁体,磁场分布已知,将一个小金属线圈套在电池上,线圈和电池构成闭合回路,通电线圈在磁场的作用下就会转动起来,从上向下附视,线圈的转动方向是( )| A. | 顺时针方向 | B. | 逆时针方向 | ||
| C. | 时而顺时针转动时而逆时针转动 | D. | 以上说法均不正确 |
4. 如图,由均匀的电阻丝组成的等边三角形导体框,垂直匀强磁场放置,将AB两点接入电压恒定的电源两端,通电时,线框受到的安培力为1.2N,若将ACB边移走,则余下线框受到的安培力大小为( )
如图,由均匀的电阻丝组成的等边三角形导体框,垂直匀强磁场放置,将AB两点接入电压恒定的电源两端,通电时,线框受到的安培力为1.2N,若将ACB边移走,则余下线框受到的安培力大小为( )
 如图,由均匀的电阻丝组成的等边三角形导体框,垂直匀强磁场放置,将AB两点接入电压恒定的电源两端,通电时,线框受到的安培力为1.2N,若将ACB边移走,则余下线框受到的安培力大小为( )
如图,由均匀的电阻丝组成的等边三角形导体框,垂直匀强磁场放置,将AB两点接入电压恒定的电源两端,通电时,线框受到的安培力为1.2N,若将ACB边移走,则余下线框受到的安培力大小为( )| A. | 0.6N | B. | 0.8N | C. | 1.2N | D. | 1.6N |
5. 如图所示为地铁站用于安全检查的装置,主要由安检传送带和x光透视系统两部分组成.在正常运行时,水平传送带的速度v是恒定的,请用物理知识判断下列说法正确的是( )
如图所示为地铁站用于安全检查的装置,主要由安检传送带和x光透视系统两部分组成.在正常运行时,水平传送带的速度v是恒定的,请用物理知识判断下列说法正确的是( )
 如图所示为地铁站用于安全检查的装置,主要由安检传送带和x光透视系统两部分组成.在正常运行时,水平传送带的速度v是恒定的,请用物理知识判断下列说法正确的是( )
如图所示为地铁站用于安全检查的装置,主要由安检传送带和x光透视系统两部分组成.在正常运行时,水平传送带的速度v是恒定的,请用物理知识判断下列说法正确的是( )| A. | 乘客把物品轻放到传送带上,物品立刻随着传送带匀速运动 | |
| B. | 乘客把物品轻放到传送带上,物品可能先向传送方向的相反方向运动 | |
| C. | 乘客把物品轻放到传送带上,物品会先做一段加速运动,这段时间的长短不只取决于传送带运行的速度v | |
| D. | 乘客把物品轻放到传送带上,物品会相对于传送带滑行一段距离,对于确定的传送带和确定的物品来说,若传送速度v提高为原来的2倍,这段距离也变为原来的2倍 |
12. 如图所示,一质量为m、电荷量为q的小球放在竖直固定的光滑绝缘圆弧轨道内.若在此空间加上平行轨道平面的匀强电场,平衡时小球与圆心的连线与竖直方向成60°角,重力加速度为g,则电场强度的最小值为( )
如图所示,一质量为m、电荷量为q的小球放在竖直固定的光滑绝缘圆弧轨道内.若在此空间加上平行轨道平面的匀强电场,平衡时小球与圆心的连线与竖直方向成60°角,重力加速度为g,则电场强度的最小值为( )
 如图所示,一质量为m、电荷量为q的小球放在竖直固定的光滑绝缘圆弧轨道内.若在此空间加上平行轨道平面的匀强电场,平衡时小球与圆心的连线与竖直方向成60°角,重力加速度为g,则电场强度的最小值为( )
如图所示,一质量为m、电荷量为q的小球放在竖直固定的光滑绝缘圆弧轨道内.若在此空间加上平行轨道平面的匀强电场,平衡时小球与圆心的连线与竖直方向成60°角,重力加速度为g,则电场强度的最小值为( )| A. | $\frac{mg}{2q}$ | B. | $\frac{mg}{q}$ | C. | $\frac{2mg}{q}$ | D. | $\frac{\sqrt{3}mg}{2q}$ |
 用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图所示,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若各落点痕迹到O的距离分别为OM=S1,OP=S2,ON=S3,并知两球的质量分别为m=10g与M=20g,则
用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图所示,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若各落点痕迹到O的距离分别为OM=S1,OP=S2,ON=S3,并知两球的质量分别为m=10g与M=20g,则
 如图所示,实线代表三根首尾相接的等长绝缘细棒,棒上的电荷分布情况与绝缘棒换成等长的细导体棒时的电荷分布完全相同.点A是△abc的中心,B点和A点相对bc边对称,已测得A、B两点的电势分别为UA和UB.现将绝缘棒ab取走,设这不影响ac、bc棒的电荷分布,试求此时A点的电势$\frac{2}{3}$UA,B点的电势$\frac{1}{6}$UA+$\frac{1}{2}$UB.
如图所示,实线代表三根首尾相接的等长绝缘细棒,棒上的电荷分布情况与绝缘棒换成等长的细导体棒时的电荷分布完全相同.点A是△abc的中心,B点和A点相对bc边对称,已测得A、B两点的电势分别为UA和UB.现将绝缘棒ab取走,设这不影响ac、bc棒的电荷分布,试求此时A点的电势$\frac{2}{3}$UA,B点的电势$\frac{1}{6}$UA+$\frac{1}{2}$UB. 将比荷不同的离子分开,是原子核物理研究中的一项重要技术.一种方法是利用如图1所示的装置,在边界AC上方存在有区域足够大的方向垂直纸面向里的匀强磁场,磁感应强度为B,边界AC上有一狭缝.离子源放射出初速度可以忽略的正离子,离子进入电场并经电场加速后,穿过狭缝沿垂直于边界AC且垂直于磁场的方向射入磁场,最后打在置有离子接收器的区域CD上被收集.已知区域CD的右边界距狭缝的距离为L,左边界距狭缝足够远,整个装置内部为真空,不计离子重力,也不考虑离子间的相互作用.
将比荷不同的离子分开,是原子核物理研究中的一项重要技术.一种方法是利用如图1所示的装置,在边界AC上方存在有区域足够大的方向垂直纸面向里的匀强磁场,磁感应强度为B,边界AC上有一狭缝.离子源放射出初速度可以忽略的正离子,离子进入电场并经电场加速后,穿过狭缝沿垂直于边界AC且垂直于磁场的方向射入磁场,最后打在置有离子接收器的区域CD上被收集.已知区域CD的右边界距狭缝的距离为L,左边界距狭缝足够远,整个装置内部为真空,不计离子重力,也不考虑离子间的相互作用.