题目内容
3.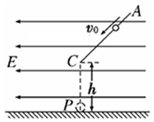 如图所示,在水平方向的匀强电场中有一表面光滑,与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量为500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处,(g=10m/s2)
如图所示,在水平方向的匀强电场中有一表面光滑,与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量为500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处,(g=10m/s2)(1)小环离开直杆后运动的加速度大小和方向;
(2)小环在直杆上匀速运动速度的大小v0.
分析 (1)根据小环在杆子上受力平衡,判断出电场力的方向,根据共点力平衡求出电场力的大小,从而得知离开杆子后所受的合力,根据牛顿第二定律求出加速度的大小和方向.
(2)小环离开直杆后做类平抛运动,利用垂直于杆的方向与沿杆的方向的位移可求出在直杆上匀速运动速度的大小v0.
解答 解:(1)小环在光滑直杆上做匀速运动,电场力必定水平向右,否则小环将做匀加速运动,其受力情况如图所示.
由平衡条件得:mgsin45°=qEcos45°…①,
解得:mg=qE,
离开直杆后,只受mg、Eq作用,则合力为:F合=$\sqrt{2}$mg=ma…②,
所以加速度为:a=2g=10$\sqrt{2}$m/s2=14.1m/s2,方向与杆垂直斜向右下方.
(2)设小环在直杆上运动的速度为v0,离杆后经t秒到达P点,则竖直方向:h=v0sin45°•t+$\frac{1}{2}g{t}^{2}$③,
水平方向:${v}_{0}cos45°×t-\frac{1}{2}\frac{qE}{m}{t}^{2}=0$…④,
联立解得:${v_0}=\sqrt{\frac{gh}{2}}=\sqrt{\frac{10×0.8}{2}}=2m/s$,
答:(1)小环离开直杆后运动的加速度大小为14.1m/s2,方向与杆垂直斜向右下方;
(2)小环在直杆上匀速运动速度的大小v0为2m/s.
点评 本题中带电粒子在电场与重力场共同作用下的运动,在直杆的束缚下的匀速直线运动与没有束缚下的类平抛运动.关键能对研究对象的受力进行正确分析,判断其运动情况,能根据其受力情况,运用运动的分解法,由运动学公式、牛顿第二定律与动能定理等物理规律求解.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
13.某物体做直线运动的v-t图象如图所示,根据图象可知( )


| A. | 0~2s内物体的加速度为2 m/s2 | |
| B. | 0~5s内物体的位移为7m | |
| C. | 物体在0~2s内与4~5s内的速度方向相同 | |
| D. | 物体在0~2s内与4~5s内的加速度方向相同 |
14.一个物体从某一高度做自由落体运动,已知它第一秒内的位移恰为它最后一秒内位移的一半,g取10m/s2,则它开始下落时距地面的高度为( )
| A. | 11.25m | B. | 15.25m | C. | 20m | D. | 31.25m |
11. 如图甲所示,AB是电场中的一条电场线,质子以某一初速度从A点出发,仅在静电力的作用下沿直线从A点运动到B点,其vt图象如图乙所示,则下列说法正确的是( )
如图甲所示,AB是电场中的一条电场线,质子以某一初速度从A点出发,仅在静电力的作用下沿直线从A点运动到B点,其vt图象如图乙所示,则下列说法正确的是( )
 如图甲所示,AB是电场中的一条电场线,质子以某一初速度从A点出发,仅在静电力的作用下沿直线从A点运动到B点,其vt图象如图乙所示,则下列说法正确的是( )
如图甲所示,AB是电场中的一条电场线,质子以某一初速度从A点出发,仅在静电力的作用下沿直线从A点运动到B点,其vt图象如图乙所示,则下列说法正确的是( )| A. | 质子运动的加速度随时间逐渐减小 | |
| B. | 电场线的方向由B点指向A点 | |
| C. | A、B两点的电场强度的大小关系满足EA<EB | |
| D. | A、B两点的电势关系满足φA<φB |
15. 如图所示,质量为2kg的物体与水平地面间动摩擦因数为0.2,水平地面足够大.t=0时,物体以2m/s初速向右运动,同时对物体施加一个水平向左的大小恒为2N的拉力F,向右为正方向,在t=0之后( )
如图所示,质量为2kg的物体与水平地面间动摩擦因数为0.2,水平地面足够大.t=0时,物体以2m/s初速向右运动,同时对物体施加一个水平向左的大小恒为2N的拉力F,向右为正方向,在t=0之后( )
 如图所示,质量为2kg的物体与水平地面间动摩擦因数为0.2,水平地面足够大.t=0时,物体以2m/s初速向右运动,同时对物体施加一个水平向左的大小恒为2N的拉力F,向右为正方向,在t=0之后( )
如图所示,质量为2kg的物体与水平地面间动摩擦因数为0.2,水平地面足够大.t=0时,物体以2m/s初速向右运动,同时对物体施加一个水平向左的大小恒为2N的拉力F,向右为正方向,在t=0之后( )| A. | 物体所受摩擦力不会变化 | B. | 物体所受摩擦力会由-4N变为+2N | ||
| C. | 物体所受摩擦力会由-4N变为-2N | D. | 物体所受摩擦力会由+4N变为+2N |
9.下列说法正确的是( )
| A. | 一般分子直径的数量级是10-8cm | |
| B. | 布朗运动是液体分子的无规则运动 | |
| C. | 气体分子速率呈现“中间多,两头少”的分布规律 | |
| D. | 两个分子由距离很远逐渐靠近到很难再靠近的过程中,分子间的作用力的大小将先减小后增大 | |
| E. | 如果两个系统分别与状态确定的第三个系统达到热平衡,那么这两个系统之间也必定达到热平衡 |
 一个重G1=400N的小孩,站在一块重G2=200N的木块上,用一根绕过光滑定滑轮的轻绳拉住木块,使小孩和木块相对静止一起匀速前进(如图所示),已知小孩的拉力F=120N,则
一个重G1=400N的小孩,站在一块重G2=200N的木块上,用一根绕过光滑定滑轮的轻绳拉住木块,使小孩和木块相对静止一起匀速前进(如图所示),已知小孩的拉力F=120N,则 如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点.设OM=L,ON=2L,求:
如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点.设OM=L,ON=2L,求: