题目内容
14.一个物体从某一高度做自由落体运动,已知它第一秒内的位移恰为它最后一秒内位移的一半,g取10m/s2,则它开始下落时距地面的高度为( )| A. | 11.25m | B. | 15.25m | C. | 20m | D. | 31.25m |
分析 由自由落体的位移公式可求得第一秒内物体通过的位移;则通过第一秒与最后一秒中通过位移的关系可得出最后一秒的位移;则可设下落总时间为t,由位移与时间的关系可列出方程解出时间,则可求得下落时距地高度.
解答 解:由h=$\frac{1}{2}$gt2可得:
第1秒内的位移h1=$\frac{1}{2}$×10m/s2×(1s)2=5m;
则最后一秒内的位移h2=2h1=10m;
则设下落总时间为t,
最后1s内的位移h=$\frac{1}{2}$gt2-$\frac{1}{2}$g(t-1)2=10m;
解得:t=1.5s;
则物体下落的总高度h=$\frac{1}{2}$gt2=11.25m.
故选:A.
点评 解决自由落体运动的题目关键在于明确自由落体中的公式应用,一般情况下,研究由落点开始的运动列出的表达式最为简单;并且最好尝试一题多解的方法.

练习册系列答案
相关题目
5. 如图所示,一个闭合线圈放在匀强磁场中,线圈的轴线与磁场方向成30°角,磁感应强度B,用下述哪个方法可使线圈的磁通量增加一倍( )
如图所示,一个闭合线圈放在匀强磁场中,线圈的轴线与磁场方向成30°角,磁感应强度B,用下述哪个方法可使线圈的磁通量增加一倍( )
 如图所示,一个闭合线圈放在匀强磁场中,线圈的轴线与磁场方向成30°角,磁感应强度B,用下述哪个方法可使线圈的磁通量增加一倍( )
如图所示,一个闭合线圈放在匀强磁场中,线圈的轴线与磁场方向成30°角,磁感应强度B,用下述哪个方法可使线圈的磁通量增加一倍( )| A. | 把线圈匝数增加一倍 | B. | 把线圈面积增加一倍 | ||
| C. | 把线圈的半径增加一倍 | D. | 转动线圈使得轴线与磁场方向平行 |
2.如图所示,一木块静止在倾角为θ的斜面上,那么木块对斜面的作用力的方向为( )
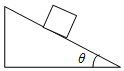

| A. | 竖直向下 | B. | 沿斜面向下 | C. | 沿斜面向上 | D. | 垂直于斜面向下 |
9.电荷+Q激发的电场中有A、B两点.质量为m,电量为q的带正电的粒子,自A点由静止释放,经过B点时的速度为v0;若此粒子的质量为2q,质量为4m,仍从A点由静止释放(粒子重力均不计),则经过B点时的速度变为( )
| A. | 2v0 | B. | 4v0 | C. | $\frac{{v}_{0}}{2}$ | D. | $\frac{v_0}{{\sqrt{2}}}$ |
19. 质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
 质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )| A. | 小球带负电 | |
| B. | 小球在斜面上运动时做加速度增大,而速度也增大的变加速直线运动 | |
| C. | 小球在斜面上运动时做匀加速直线运动 | |
| D. | 小球在斜面上下滑过程中,当小球对斜面压力为零时的速率为$\frac{mgsinθ}{qB}$ |
6. 如图所示,AB为固定的光滑圆弧轨道,O为圆心,AO水平,BO竖直,轨道半径为R,将质量为m的小球(可视为质点)从A点由静止释放,在小球从A点运动到B点的过程中,小球( )
如图所示,AB为固定的光滑圆弧轨道,O为圆心,AO水平,BO竖直,轨道半径为R,将质量为m的小球(可视为质点)从A点由静止释放,在小球从A点运动到B点的过程中,小球( )
 如图所示,AB为固定的光滑圆弧轨道,O为圆心,AO水平,BO竖直,轨道半径为R,将质量为m的小球(可视为质点)从A点由静止释放,在小球从A点运动到B点的过程中,小球( )
如图所示,AB为固定的光滑圆弧轨道,O为圆心,AO水平,BO竖直,轨道半径为R,将质量为m的小球(可视为质点)从A点由静止释放,在小球从A点运动到B点的过程中,小球( )| A. | 所受合力的冲量水平向右 | B. | 所受支持力的冲量水平向右 | ||
| C. | 所受合力的冲量大小为m$\sqrt{2gR}$ | D. | 所受重力的冲量大小为0 |
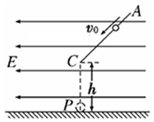 如图所示,在水平方向的匀强电场中有一表面光滑,与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量为500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处,(g=10m/s2)
如图所示,在水平方向的匀强电场中有一表面光滑,与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量为500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处,(g=10m/s2)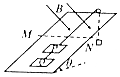 如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长及P线框最上边到MN的距离均为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,sin37°=0.6,cos37°=0.8,求:
如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长及P线框最上边到MN的距离均为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,sin37°=0.6,cos37°=0.8,求: