题目内容
14.某一行星有一卫星,以半径r,周期T做匀速圆周运动,已知引力常量为G,求:(1)行星的质量;
(2)若行星的半径为R,则行星密度为多少.
分析 据万有引力等于向心力,可以列式求解出行星的质量,进一步求出密度.
解答 解:(1)设行星质量为M,卫星质量为m,行星对卫星的万有引力提供向心力,则:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$;
(2)由于M=ρV,
所以ρ=$\frac{M}{V}$=$\frac{3{πr}^{3}}{{{GT}^{2}R}^{3}}$.
答:(1)行星的质量是$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$;
(2)若行星的半径为R,则行星密度为$\frac{3{πr}^{3}}{{{GT}^{2}R}^{3}}$.
点评 本题关键要掌握万有引力等于向心力列出等式求解.要注意轨道半径和星球半径的关系.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2.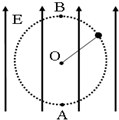 如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )
如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )
 如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )
如图所示,轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中,使小球以悬点O为圆心在竖直平面内做完整的圆周运动,则( )| A. | 小球一定做变速圆周运动 | |
| B. | 小球可能做匀速圆周运动 | |
| C. | 小球经过最低点A时绳子拉力一定最小 | |
| D. | 小球经过最高点B时绳子拉力可能最大 |
9.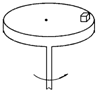 质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )
质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )
 质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )
质量为m的物体置于一个水平转台上,物体距转轴为r,当转速为ω时,物体与转台相对静止,如图.那么,下列说法中正确的是( )| A. | 物体受重力、弹力、摩擦力和向心力作用 | |
| B. | 物体所受摩擦力在圆轨道的切线方向,与线速度方向相反 | |
| C. | 物体所受摩擦力指向圆心,提供物体运动所需的向心力 | |
| D. | 物体不受摩擦力的作用 |
3.两个电子以大小不同的初速度沿垂直磁场的方向射入同一匀强磁场中,设r1、r2为这两个电子的运动轨道半径,T1、T2是它们的运动周期,则( )
| A. | r1=r2 T1≠T2 | B. | r1≠r2 T1≠T2 | C. | r1=r2 T1=T2 | D. | r1≠r2 T1=T2 |
4.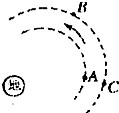 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )| A. | 线速度大小的关系是VA<VB=VC | |
| B. | 周期关系是TA>TB=TC | |
| C. | 向心力大小的关系是FA=FB<FC | |
| D. | 轨道半径和周期的关系是$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
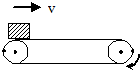 一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.
一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.