题目内容
5.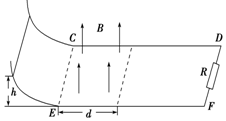 CD、EF是两条水平放置的阻值可忽略的平行金属导轨,导轨间距为L,在水平导轨的左侧存在磁感应强度方向垂直导轨平面向上的匀强磁场,磁感应强度大小为B,磁场区域的宽度为d,如图所示.导轨的右端接有一阻值为R的电阻,左端与一弯曲的光滑轨道平滑连接.将一阻值也为R,质量为m的导体棒从弯曲轨道上h高处由静止释放,导体棒最终恰好停在磁场的右边界处.已知导体棒与水平导轨接触良好,且动摩擦因数为μ,则下列说法中正确的是( )
CD、EF是两条水平放置的阻值可忽略的平行金属导轨,导轨间距为L,在水平导轨的左侧存在磁感应强度方向垂直导轨平面向上的匀强磁场,磁感应强度大小为B,磁场区域的宽度为d,如图所示.导轨的右端接有一阻值为R的电阻,左端与一弯曲的光滑轨道平滑连接.将一阻值也为R,质量为m的导体棒从弯曲轨道上h高处由静止释放,导体棒最终恰好停在磁场的右边界处.已知导体棒与水平导轨接触良好,且动摩擦因数为μ,则下列说法中正确的是( )| A. | 电阻R的最大电流为$\frac{BL\sqrt{2gh}}{2R}$ | B. | 流过电阻R的电荷量为$\frac{BdL}{2R}$ | ||
| C. | 整个电路中产生的焦耳热为mgh | D. | 电阻R中产生的焦耳热为$\frac{1}{2}$mg(h-μd) |
分析 金属棒在弯曲轨道下滑时,只有重力做功,机械能守恒,由机械能守恒定律或动能定理可以求出金属棒到达水平面时的速度,由E=BLv求出感应电动势,然后求出感应电流;由q=$\frac{△Φ}{R+r}$可以求出感应电荷量;克服安培力做功转化为焦耳热,由动能定理(或能量守恒定律)可以求出克服安培力做功,得到导体棒产生的焦耳热.
解答 解:A、金属棒下滑过程中,机械能守恒,由机械能守恒定律得:mgh=$\frac{1}{2}$mv2,金属棒到达水平面时的速度v=$\sqrt{2gh}$,金属棒到达水平面后进入磁场受到向左的安培力做减速运动,则刚到达水平面时的速度最大,所以最大感应电动势为 E=BLv,最大的感应电流为 I=$\frac{BLv}{2R}$=$\frac{BL\sqrt{2gh}}{2R}$,故A正确;
B、通过金属棒的电荷量 q=$\frac{△Φ}{R+r}$=$\frac{BLd}{2R}$,故B正确;
C、金属棒在整个运动过程中,由动能定理得:mgh-WB-μmgd=0-0,则克服安培力做功:WB=mgh-μmgd,故C错误;
D、克服安培力做功转化为焦耳热,电阻与导体棒电阻相等,通过它们的电流相等,则金属棒产生的焦耳热:QR=$\frac{1}{2}$Q=$\frac{1}{2}$WB=$\frac{1}{2}$(mgh-μmgd),故D正确.
故选:ABD
点评 本题关键要熟练推导出感应电荷量的表达式q=$\frac{△Φ}{R+r}$,这是一个经验公式,经常用到,要在理解的基础上记住,同时涉及到能量时优先考虑功能关系,能正确分析能量转化方向是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
13.让质子和氘的混合物沿着与电场垂直的方向进入匀强电场,要使它们最后的偏转角相同,这些粒子进入电场时必须具有相同的( )
| A. | 初速度 | B. | 动量(mv) | C. | 动能 | D. | 质量 |
20. 如图甲所示,两平行金属板竖直放置,左极板接地,中间有小孔,右极板电势随时间变 化的规律如图乙,电子原来静止在左极板小孔处,不计电子的重力,下列说法正确的是( )
如图甲所示,两平行金属板竖直放置,左极板接地,中间有小孔,右极板电势随时间变 化的规律如图乙,电子原来静止在左极板小孔处,不计电子的重力,下列说法正确的是( )
 如图甲所示,两平行金属板竖直放置,左极板接地,中间有小孔,右极板电势随时间变 化的规律如图乙,电子原来静止在左极板小孔处,不计电子的重力,下列说法正确的是( )
如图甲所示,两平行金属板竖直放置,左极板接地,中间有小孔,右极板电势随时间变 化的规律如图乙,电子原来静止在左极板小孔处,不计电子的重力,下列说法正确的是( )| A. | 若 t=0 时刻释放电子,电子始终向右运动,直到打到右极板上 | |
| B. | 若 t=0 时刻释放电子,电子可能在两板间振动 | |
| C. | 若 t=$\frac{T}{4}$ 时刻释放电子,电子可能在两板间振动,也可能打到右极板上 | |
| D. | 若 t=$\frac{3T}{8}$ 时刻释放电子,电子必然打到左极板上 |
10.汽车以20m/s的速度在平直公路上行驶,急刹车时的加速度大小为5m/s2,则自驾驶员急踩刹车开始,6s内和最后2s内汽车的位移之比为( )
| A. | 1:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
17.如图所示是某电场区域的电场线分布,A、B、C、D 是电场中的四点,场强 E 的大小关系正确的是( )

| A. | EA<EC | B. | EB>ED | C. | EC<ED | D. | ED<EA |
14.在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间.计时器所用电源的频率为50Hz,每隔0.02秒打一次点.图1为一次实验得到的一条纸带,纸带上每相邻的两计数点间都有四个点未画出,按时间顺序取0、1、2、3、4、5六个计数点,用刻度尺量出1、2、3、4、5点到0点的距离如图所示(单位:cm).由纸带数据计算可得:

①小车的加速度大小a=0.76m/s2.(要求把所有数据都用上,结果保留两位有效数字)
②试根据纸带上各个计数点间的距离,计算出打下1、2、3、4、5五个点时小车的瞬时速度,并将各个速度值填入表中.(要求保留两位有效数字)
③将1、2、3、4、5各个时刻的瞬时速度标在直角坐标系中,并在图2中画出小车的瞬时速度随时间变化的关系线.
④0点的速度不是(填写是或者不是)为零.

①小车的加速度大小a=0.76m/s2.(要求把所有数据都用上,结果保留两位有效数字)
②试根据纸带上各个计数点间的距离,计算出打下1、2、3、4、5五个点时小车的瞬时速度,并将各个速度值填入表中.(要求保留两位有效数字)
| v1 | v2 | v3 | v4 | v5 | |
| 数值/(m•s-1) | 0.18 | 0.25 | 0.41 | 0.48 |
④0点的速度不是(填写是或者不是)为零.
15.真空中两金属小球所带电荷量分别为+5Q和-Q,将它们接触后再分开,距离为r.真空中的静电力常量用k表示,则此时这两个金属小球之间的库仑力为( )
| A. | k$\frac{{Q}^{2}}{{r}^{2}}$ | B. | k$\frac{5{Q}^{2}}{{r}^{2}}$ | C. | k$\frac{4{Q}^{2}}{{r}^{2}}$ | D. | k$\frac{2{Q}^{2}}{{r}^{2}}$ |

 如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、有效电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)
如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、有效电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)