题目内容
2. 如图所示,质量相等的A、B两小球分别连在弹簧两端,B小球用细绳固定在倾角为30°的光滑斜面上,若不计算弹簧质量,在细绳被剪断的瞬间,关于A、B两小球的加速度大小,正确的是( )
如图所示,质量相等的A、B两小球分别连在弹簧两端,B小球用细绳固定在倾角为30°的光滑斜面上,若不计算弹簧质量,在细绳被剪断的瞬间,关于A、B两小球的加速度大小,正确的是( )| A. | aA=g | B. | aA=0.5g | C. | aB=g | D. | aB=0.5g |
分析 在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变,再分别对A、B两个小球运用牛顿第二定律,即可求得加速度.
解答 解:AB、在剪断绳子之前,A处于平衡状态,所以弹簧的拉力等于A的重力沿斜面的分力相等.在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变仍为A的重力沿斜面上的分力.故A球的加速度为零,aA=0,故AB错误;
BD、在剪断绳子之前,对B球进行受力分析,B受到重力、弹簧对它斜向下的拉力、支持力及绳子的拉力,在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,对B球进行受力分析,则B受到到重力、弹簧的向下拉力、支持力.所以根据牛顿第二定律得:aB=$\frac{mgsin30°+mgsinsin30°}{m}$=g,故C正确,D错误;
故选:C.
点评 该题要注意在剪断绳子的瞬间,绳子上的力立即减为0,而弹簧的弹力不发生改变,再结合牛顿第二定律解题,难度不大.

练习册系列答案
相关题目
12. 如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )
如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )
 如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )
如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )| A. | 物体所受摩擦力方向平行于斜面沿虚线向上 | |
| B. | 物体与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| C. | 物体所受摩擦力方向与水平推力垂直且平行斜面向上 | |
| D. | 物体与斜面间的动摩擦因数μ=$\frac{\sqrt{6}}{3}$ |
10. 如图所示,水平细杆上套一细环A、环A与球B间用一轻质绳相连,质量分别为mA、mB,由于B球受到水平恒力F的作用,A环与B球一起向右匀速运动,绳与竖直方向的夹角为θ,则下列说法正确的是( )
如图所示,水平细杆上套一细环A、环A与球B间用一轻质绳相连,质量分别为mA、mB,由于B球受到水平恒力F的作用,A环与B球一起向右匀速运动,绳与竖直方向的夹角为θ,则下列说法正确的是( )
 如图所示,水平细杆上套一细环A、环A与球B间用一轻质绳相连,质量分别为mA、mB,由于B球受到水平恒力F的作用,A环与B球一起向右匀速运动,绳与竖直方向的夹角为θ,则下列说法正确的是( )
如图所示,水平细杆上套一细环A、环A与球B间用一轻质绳相连,质量分别为mA、mB,由于B球受到水平恒力F的作用,A环与B球一起向右匀速运动,绳与竖直方向的夹角为θ,则下列说法正确的是( )| A. | B球受到的恒力F小为mAg+tanθ | |
| B. | 绳对B球的拉力为$\frac{{m}_{B}g}{sinθ}$ | |
| C. | 杆对A环的弹力为(mA+mB)g | |
| D. | A环与杆的动摩擦因数为$\frac{{m}_{B}}{{m}_{A}+{m}_{B}}$tanθ |
17. 如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,木块处于匀速直线运动状态,F1=10N,F2=2N,若撤去F1的瞬间木块受到合力F和摩擦力f的大小、方向以及以后物体的运动情况分别是( )
如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,木块处于匀速直线运动状态,F1=10N,F2=2N,若撤去F1的瞬间木块受到合力F和摩擦力f的大小、方向以及以后物体的运动情况分别是( )
 如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,木块处于匀速直线运动状态,F1=10N,F2=2N,若撤去F1的瞬间木块受到合力F和摩擦力f的大小、方向以及以后物体的运动情况分别是( )
如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,木块处于匀速直线运动状态,F1=10N,F2=2N,若撤去F1的瞬间木块受到合力F和摩擦力f的大小、方向以及以后物体的运动情况分别是( )| A. | F=0;f=2N,方向向右 | B. | F=10N,方向向左;f=8N,方向向左 | ||
| C. | F=10N,方向向左;f=8N,方向向右 | D. | 物体做匀减速直线运动,最后静止 |
7. 如图所示,把质量为m的球夹在竖直墙壁AC和木板BC之间,不计摩擦,绕C点将板BC缓慢放至水平的过程中,下列说法正确的是( )
如图所示,把质量为m的球夹在竖直墙壁AC和木板BC之间,不计摩擦,绕C点将板BC缓慢放至水平的过程中,下列说法正确的是( )
 如图所示,把质量为m的球夹在竖直墙壁AC和木板BC之间,不计摩擦,绕C点将板BC缓慢放至水平的过程中,下列说法正确的是( )
如图所示,把质量为m的球夹在竖直墙壁AC和木板BC之间,不计摩擦,绕C点将板BC缓慢放至水平的过程中,下列说法正确的是( )| A. | 球对墙的压力减小 | B. | 球对墙的压力增大 | ||
| C. | 球对板的压力减小 | D. | 球对板的压力先增大后减小 |
14.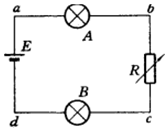 如图所示电路中灯泡A、B均不亮,但电路中只有一处断开,现作电压表测得Uab=0、Uac=0、Ubd=3V、Ucd=3V,则可分析出( )
如图所示电路中灯泡A、B均不亮,但电路中只有一处断开,现作电压表测得Uab=0、Uac=0、Ubd=3V、Ucd=3V,则可分析出( )
 如图所示电路中灯泡A、B均不亮,但电路中只有一处断开,现作电压表测得Uab=0、Uac=0、Ubd=3V、Ucd=3V,则可分析出( )
如图所示电路中灯泡A、B均不亮,但电路中只有一处断开,现作电压表测得Uab=0、Uac=0、Ubd=3V、Ucd=3V,则可分析出( )| A. | B灯断开 | B. | A灯断开 | C. | 电源断开 | D. | R断开 |
 一水平轨道AB距离地面的高度为H=0.8m,A、B点间的距离为2.5m,一长度合适的薄木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=45°的斜面,如图所示.一质量为m=1kg的小物体,在水平轨道上运动,小物体与轨道AB间的动摩擦因数μ=0.2,设小物体从B点水平抛出时的速度为vB.(不计空气阻力,不考虑物体碰撞木板或地面后的运动,取g=10m/s2)
一水平轨道AB距离地面的高度为H=0.8m,A、B点间的距离为2.5m,一长度合适的薄木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=45°的斜面,如图所示.一质量为m=1kg的小物体,在水平轨道上运动,小物体与轨道AB间的动摩擦因数μ=0.2,设小物体从B点水平抛出时的速度为vB.(不计空气阻力,不考虑物体碰撞木板或地面后的运动,取g=10m/s2) 如图,一小砝码静置于水平桌面的桌布上,高桌布左边缘和桌子的右边缘的间距均为d,已知砝码与桌布间的动摩擦因数为μ1,砝码与桌面间的动摩擦因数为μ2,现突然以恒定水平向右的加速度a将桌面抽离桌面,为了确保砝码不会从桌面上掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
如图,一小砝码静置于水平桌面的桌布上,高桌布左边缘和桌子的右边缘的间距均为d,已知砝码与桌布间的动摩擦因数为μ1,砝码与桌面间的动摩擦因数为μ2,现突然以恒定水平向右的加速度a将桌面抽离桌面,为了确保砝码不会从桌面上掉下,则加速度a满足的条件是什么?(以g表示重力加速度)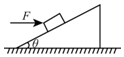 如图所示,斜面倾角θ,斜面底端有一质量为m的物体,物体与斜面间的滑动摩擦系数μ,今用一水平力F使物体向上运动,求物体的加速度.
如图所示,斜面倾角θ,斜面底端有一质量为m的物体,物体与斜面间的滑动摩擦系数μ,今用一水平力F使物体向上运动,求物体的加速度.