题目内容
6.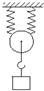 如图所示,两根原长相同的轻弹簧竖直悬挂,其下端用一根跨过动滑轮的细绳连在一起,不计绳与滑轮质量,两弹簧原来均无形变,在动滑轮下挂一质量为m的砝码后,动滑轮下降的高度多大?已知两根弹簧的劲度系数分别为k1和k2,弹簧始终保持弹性形变,细线均呈竖直方向.?
如图所示,两根原长相同的轻弹簧竖直悬挂,其下端用一根跨过动滑轮的细绳连在一起,不计绳与滑轮质量,两弹簧原来均无形变,在动滑轮下挂一质量为m的砝码后,动滑轮下降的高度多大?已知两根弹簧的劲度系数分别为k1和k2,弹簧始终保持弹性形变,细线均呈竖直方向.?
分析 根据平衡条件可知,两弹簧弹力大小相等,都为重力的一半,但由于两根弹簧的劲度系数不同,则伸长量不同,根据胡克定律结合几何关系求解即可.
解答 解:重物处于平衡状态,根据平衡条件可知,每根弹簧的弹力大小相等且为:F=$\frac{1}{2}mg$,
第一根弹簧的伸长为:$△{l}_{1}=\frac{F}{{k}_{1}}=\frac{mg}{2{k}_{1}}$,
第二根弹簧的伸长为:$△{l}_{2}=\frac{F}{{k}_{2}}=\frac{mg}{2{k}_{2}}$,
则动滑轮下降的高度为:h=$\frac{△{l}_{1}+△{l}_{2}}{2}=\frac{{k}_{1}+{k}_{2}}{4{k}_{1}{k}_{2}}mg$
答:动滑轮下降的高度为$\frac{{k}_{1}+{k}_{2}}{4{k}_{1}{k}_{2}}mg$.
点评 本题主要考查了共点力平衡条件以及胡克定律的直接应用,难度不大,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3. 一滑块在水平地面上沿直线滑行,t=0时速率为1m/s.从此刻开始在与速度平行的方向上施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,则(两图取同一正方向,取g=10m/s2)( )
一滑块在水平地面上沿直线滑行,t=0时速率为1m/s.从此刻开始在与速度平行的方向上施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,则(两图取同一正方向,取g=10m/s2)( )
 一滑块在水平地面上沿直线滑行,t=0时速率为1m/s.从此刻开始在与速度平行的方向上施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,则(两图取同一正方向,取g=10m/s2)( )
一滑块在水平地面上沿直线滑行,t=0时速率为1m/s.从此刻开始在与速度平行的方向上施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,则(两图取同一正方向,取g=10m/s2)( )| A. | 滑块的质量为0.5 kg | |
| B. | 滑块与水平地面间的动摩擦因数为0.05 | |
| C. | 第1 s内摩擦力对滑块做功为-1 J | |
| D. | 第2 s内力F的平均功率为1.5 W |
11. 一个物体以初速度v0从A点开始在光滑水平面上运动.一个水平力作用在物体上,物体的运动轨迹如图中实线所示,图中B为轨迹上一点,虚线是过A、B两点并与运动轨迹相切的直线,虚线和实线将水平面划分为图示的5个区域.则关于该施力物体位置的判断,下列说法中正确的是( )
一个物体以初速度v0从A点开始在光滑水平面上运动.一个水平力作用在物体上,物体的运动轨迹如图中实线所示,图中B为轨迹上一点,虚线是过A、B两点并与运动轨迹相切的直线,虚线和实线将水平面划分为图示的5个区域.则关于该施力物体位置的判断,下列说法中正确的是( )
 一个物体以初速度v0从A点开始在光滑水平面上运动.一个水平力作用在物体上,物体的运动轨迹如图中实线所示,图中B为轨迹上一点,虚线是过A、B两点并与运动轨迹相切的直线,虚线和实线将水平面划分为图示的5个区域.则关于该施力物体位置的判断,下列说法中正确的是( )
一个物体以初速度v0从A点开始在光滑水平面上运动.一个水平力作用在物体上,物体的运动轨迹如图中实线所示,图中B为轨迹上一点,虚线是过A、B两点并与运动轨迹相切的直线,虚线和实线将水平面划分为图示的5个区域.则关于该施力物体位置的判断,下列说法中正确的是( )| A. | 如果这个力是引力,则施力物体一定在④区域 | |
| B. | 如果这个力是引力,则施力物体一定在②区域 | |
| C. | 如果这个力是斥力,则施力物体一定在⑤区域 | |
| D. | 如果这个力是斥力,则施力物体可能在①或③区域 |
18.关于原子结构及原子核的知识,下列判断正确的是( )
| A. | 每一种原子都有自己的特征谱线 | |
| B. | α射线的穿透能力比γ射线弱 | |
| C. | γ射线是原子核受到激发后产生的 | |
| D. | 放射性元素的半衰期可能与压力、温度有关 |
15.下列说法正确的( )
| A. | ${\;}_{90}^{234}$Th→${\;}_{91}^{234}$Pa+X 中的X是中子 | |
| B. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H 是α衰变 | |
| C. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n 是核聚变 | |
| D. | ${\;}_{34}^{82}$Se→${\;}_{36}^{82}$Kr+2${\;}_{-1}^{0}$e 是核裂变 |
16.如图甲所示,轻杆一端与质量为0.3kg、可视为质点的小球相连,另一端可绕光滑固定轴在竖直平面内自由转动.现使小球在竖直平面内做圆周运动,经最高点开始计时,取水平向右为正方向,小球的水平分速度v随时间t的变化关系如图乙所示,A、B、C三点分别是图线与纵轴、横轴的交点、图线上第一周期内的最低点,该三点的纵坐标分别是1、0、-5.g取10m/s2,不计空气阻力.下列说法中正确的是( )


| A. | B点对应时刻,小球速度为零 | |
| B. | 小球在竖直面内圆周运动的周期3.0 s | |
| C. | AB段图线与坐标轴所围的面积为0.6m | |
| D. | 小球经过最高点时,杆对它的作用力大小为2.5N,方向竖直向上 |
 如图所示,两木块的质量为m、M,中间弹簧的劲度系数为k,弹簧下端与M连接,m与弹簧不连接,现将m下压一段距离释放,它就上下做简谐运动,振动过程中,m始终没有离开弹簧.试求:
如图所示,两木块的质量为m、M,中间弹簧的劲度系数为k,弹簧下端与M连接,m与弹簧不连接,现将m下压一段距离释放,它就上下做简谐运动,振动过程中,m始终没有离开弹簧.试求: 如图所示,在长为100$\sqrt{3}$m的跑道上静止放有质量m=50kg的木箱,已知木箱与跑道间的摩擦系数为μ=$\frac{\sqrt{3}}{3}$,今给物体施加一大小为F=500N的力作用.求:
如图所示,在长为100$\sqrt{3}$m的跑道上静止放有质量m=50kg的木箱,已知木箱与跑道间的摩擦系数为μ=$\frac{\sqrt{3}}{3}$,今给物体施加一大小为F=500N的力作用.求: