题目内容
4.在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下:A.取一根符合实验要求的摆线,下端系一金属小球,上端固定在O点;
B.在小球静止悬挂时测量出O点到小球球心的距离L;
C.拉动小球使细线偏离竖直方向一个不大的角度(约5°),然后由静止释放小球;
D.用秒表记录小球完成n次全振动所用的时间t
(1)用所测物理量的符号表示重力加速度的测量值,其表达式为g=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$.;
(2)若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能是C(选填下列选项前的序号)
A.测量摆长时,把摆线的长度当成了摆长
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长
C.测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=$\frac{t}{n}$求得周期
D.摆球的质量过大
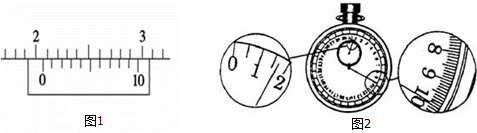
(3)用游标上有10个小格的游标卡尺测量摆球直径如图1所示,摆球直径为2.06cm.然后用秒表记录了单摆振动50次所用的时间如图2所示,秒表读数为100.0 s.
分析 (1)根据单摆的周期公式,结合周期的大小求出重力加速度的表达式.
(2)根据重力加速度的表达式,结合摆长或周期的测量误差确定重力加速度的测量误差.
(3)游标卡尺的读数等于主尺读数加上游标读数,不需估读;秒表的读数等于小盘读数加上大盘读数.
解答 解:(1)单摆的周期T=$\frac{t}{n}$,根据T=$2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$.
(2)根据T=$2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,
A、测量摆长时,把摆线的长度当成了摆长,则摆长的测量值偏小,导致重力加速度的测量值偏小,故A错误.
B、摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长,知摆长的测量值偏小,导致重力加速度测量值偏小,故B错误.
C、测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,则周期的测量值偏小,导致重力加速度的测量值偏大,故C正确.
D、摆球的质量过大,不影响重力加速度的测量,故D错误.
故选:C.
(3)游标卡尺的主尺读数为20mm,游标读数为0.1×6mm=0.6mm,则最终读数为20.6mm=2.06cm.
秒表的小盘读数为90s,大盘读数为 10.0s,则秒表读数为100.0s.
故答案为:(1)$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$,(2)C,(3)2.06,100.0.
点评 解决本题的关键掌握单摆的周期公式,知道影响测量重力加速度误差的因素,掌握游标卡尺和秒表的读数方法,难度不大.

练习册系列答案
相关题目
14.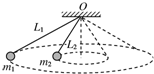 如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )
如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )
 如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )
如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )| A. | 两小球做匀速圆周运动的角速度相等 | |
| B. | 两小球做匀速圆周运动的线速度相等 | |
| C. | 两小球的质量比一定是m1:m2=$\sqrt{3}$:1 | |
| D. | L2细线跟竖直方向成45°角 |
12.2007年10月24日18时05分,中国第一颗探月卫星“嫦娥一号”在西昌卫星发射中心成功升空,已知月球半径为R,若“嫦娥一号”到达距月球表面高为2R处时,地面控制中心将其速度调整为v时恰能绕月球匀速飞行,将月球视为质量分布均匀的球体,则月球表面的重力加速度为( )
| A. | $\frac{{v}^{2}}{R}$ | B. | $\frac{2{v}^{2}}{R}$ | C. | $\frac{3{v}^{2}}{R}$ | D. | $\frac{4{v}^{2}}{R}$ |
19.匀速圆周运动在科学史上曾经起过重要作用.下面列举的四位学者,关于匀速圆周运动的论述,现在看来仍然正确的是( )
| A. | 古希腊思想家柏拉图认为“天体的运动是圆周运动,因为圆周运动是最完善的,不需要任何推动” | |
| B. | 德国天文学家开普勒认为“火星轨道不是一个圆周,而是一个椭圆,并且没有这样一点,火星绕该点的运动是匀速的” | |
| C. | 意大利物理学家伽利略在《两门新科学的对话》一书中指出:“任何速度一旦施加给一个运动着的物体,只要除去加速或减速的外因,此速度就可以保持不变,不过这是只能在水平而发生的一种情形.”他所说的“水平面”是指和球心等距离的球面 | |
| D. | 英国科学家牛顿认为:匀速圆周运动的物体受到的向心力指向圆心,向心力的大小与单位时间内通过的弧长的平方成正比,与圆周轨道半径成反比 |
9. 如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲、乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )
如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲、乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )
 如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲、乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )
如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲、乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )| A. | 每根金属杆的电阻R=0.016Ω | |
| B. | 甲金属杆在磁场中运动的时间是0.4 s | |
| C. | 甲金属杆在磁场中运动过程中F的功率逐渐增大 | |
| D. | 乙金属杆在磁场中运动过程中安培力的功率是0.1 W |
16. 如图所示闭合线圈处在变化的磁场中,线圈中产生了顺时针方向的感应电流,而且线圈的面积有收缩的趋热,那么,线圈内磁场可能是( )
如图所示闭合线圈处在变化的磁场中,线圈中产生了顺时针方向的感应电流,而且线圈的面积有收缩的趋热,那么,线圈内磁场可能是( )
 如图所示闭合线圈处在变化的磁场中,线圈中产生了顺时针方向的感应电流,而且线圈的面积有收缩的趋热,那么,线圈内磁场可能是( )
如图所示闭合线圈处在变化的磁场中,线圈中产生了顺时针方向的感应电流,而且线圈的面积有收缩的趋热,那么,线圈内磁场可能是( )| A. | 磁场方向垂直纸面向内,且磁感应强度在减小 | |
| B. | 磁场方向垂直纸面向内,且磁感应强度在增大 | |
| C. | 磁场方向垂直纸面向外,且磁感应强度在减小 | |
| D. | 磁场方向垂直纸面向外,且磁感应强度在增大 |
13. 如图为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若质量为m的小车在平直的水泥路上从静止开始沿直线加速行驶,经过时间t前进的距离为x,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,以下判断错误的是( )
如图为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若质量为m的小车在平直的水泥路上从静止开始沿直线加速行驶,经过时间t前进的距离为x,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,以下判断错误的是( )
 如图为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若质量为m的小车在平直的水泥路上从静止开始沿直线加速行驶,经过时间t前进的距离为x,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,以下判断错误的是( )
如图为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若质量为m的小车在平直的水泥路上从静止开始沿直线加速行驶,经过时间t前进的距离为x,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为f,以下判断错误的是( )| A. | 小车做匀加速运动 | |
| B. | 小车受到的牵引力逐渐减小 | |
| C. | 小车受到的牵引力所做的功为Pt | |
| D. | 小车受到的牵引力做的功为fx+$\frac{1}{2}$mvm2 |
14.关于物体的速度和加速度的说法正确的是( )
| A. | 速度大,则其加速度大 | |
| B. | 加速度大,则其速度也大 | |
| C. | 速度变化越来越快,则加速度越大 | |
| D. | 速度变化方向可能与其加速度方向不一致 |