题目内容
1.设行星a和行星b是两个均匀球体,两行星的质量之比ma:mb=2:1,半径之比Ra:Rb=1:2.行星a的卫星绕其表面附近做圆周运动的周期为Ta,行星b的卫星绕其表面附近做圆周运动的周期为Tb,则它们的周期之比Ta:Tb为( )| A. | 1:4 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
分析 根据万有引力提供向心力得出两卫星的周期表达式,结合周期表达式得出周期之比.
解答 解:对行星a的卫星,根据万有引力提供向心力有:$G\frac{{m}_{a}m}{{{R}_{a}}^{2}}=m{R}_{a}\frac{4{π}^{2}}{{{T}_{a}}^{2}}$,解得${T}_{a}=\sqrt{\frac{4{π}^{2}{{R}_{a}}^{3}}{G{m}_{a}}}$,
对行星b的卫星,根据万有引力提供向心力有:$G\frac{{m}_{b}m}{{{R}_{b}}^{2}}=m{R}_{b}\frac{4{π}^{2}}{{{T}_{b}}^{2}}$,解得${T}_{b}=\sqrt{\frac{4{π}^{2}{{R}_{b}}^{3}}{G{m}_{b}}}$,
则$\frac{{T}_{a}}{{T}_{b}}=\sqrt{\frac{{{R}_{a}}^{3}{m}_{b}}{{{R}_{b}}^{3}{m}_{a}}}$=$\sqrt{\frac{1}{8}×\frac{1}{2}}=\frac{1}{4}$.
故选:A.
点评 解决本题的关键掌握 万有引力提供向心力这一重要理论,并能灵活运用,基础题.

练习册系列答案
相关题目
11.若用打点计时器做探究碰撞中的不变量实验时,下列哪些操作是正确的( )
| A. | 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了改变两车的质量 | |
| B. | 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了碰撞后粘在一起 | |
| C. | 先接通打点计时器电源,再释放拖动纸带的小车 | |
| D. | 先释放拖动纸带的小车,再接通打点计时器的电源 |
16.下列关于物体做斜抛运动的叙述,正确的是( )
| A. | 物体受到变力作用,且力的方向与初速度不在一条直线 | |
| B. | 物体受到恒力作用,且力的方向与初速度垂直时,物体做斜抛运动 | |
| C. | 物体受到恒力作用,且力的方向与初速度不在一条直线上,物体一定做斜抛运动 | |
| D. | 物体只受重力作用,且力的方向与初速度不在一条直线 上,也不垂直时,物体一定做斜抛运动 |
6. 如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
 如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )| A. | 粒子A带正电,B不带电,C带负电 | |
| B. | 三个粒子在电场中运动时间相等 | |
| C. | 三个粒子在电场中运动的加速度aA<aB<aC | |
| D. | 三个粒子到达极板时的动能EKA<EKB<EKC |
13.关于弹性势能,下列说法正确的是( )
| A. | 弹性势能与物体的形变量有关 | |
| B. | 弹性势能与物体的形变量无关 | |
| C. | 物体运动的速度越大,弹性势能越大 | |
| D. | 弹性势能与物体的速度无关 |
10. 图示中交流电流表A1、A2、A3分别与电容器,线圈L和电阻R串联后接在同一交流电源上,供电电压瞬时值为u1=Umsinω1t.三个电流表各有不同的读数,现换另一个电源供电,供电电压瞬时值为u2=Umsinω2t,其中ω2=2ω1.改换电源后三个电流表的度数变化情况是( )
图示中交流电流表A1、A2、A3分别与电容器,线圈L和电阻R串联后接在同一交流电源上,供电电压瞬时值为u1=Umsinω1t.三个电流表各有不同的读数,现换另一个电源供电,供电电压瞬时值为u2=Umsinω2t,其中ω2=2ω1.改换电源后三个电流表的度数变化情况是( )
 图示中交流电流表A1、A2、A3分别与电容器,线圈L和电阻R串联后接在同一交流电源上,供电电压瞬时值为u1=Umsinω1t.三个电流表各有不同的读数,现换另一个电源供电,供电电压瞬时值为u2=Umsinω2t,其中ω2=2ω1.改换电源后三个电流表的度数变化情况是( )
图示中交流电流表A1、A2、A3分别与电容器,线圈L和电阻R串联后接在同一交流电源上,供电电压瞬时值为u1=Umsinω1t.三个电流表各有不同的读数,现换另一个电源供电,供电电压瞬时值为u2=Umsinω2t,其中ω2=2ω1.改换电源后三个电流表的度数变化情况是( )| A. | A2、A3的读数不变 | B. | A1、A3的读数不变 | C. | A1、A3的读数增大 | D. | 仅A1的读数增大 |
17. 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为2R | |
| B. | 小球落地点时的动能为$\frac{5mgR}{2}$ | |
| C. | 小球运动到半圆弧最高点P时向心力恰好为零 | |
| D. | 小球在o点的支持力为2mg |
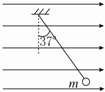 一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求:
一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求: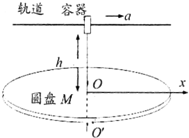 如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴OO′匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=5m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)
如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴OO′匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=5m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)