题目内容
12.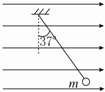 一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求:
一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求:(1)小球的电性及匀强电场的电场强度的大小;
(2)若剪断丝线,小球将作什么运动?并求出小球从剪断丝线开始到到达地面经过的时间t.
分析 (1)小球受到重力、电场力和拉力而平衡,作出受力图,根据平衡条件求解电场强度E.
(2)剪断丝线后,小球受到重力、电场力作用,这两个力是恒力,它们的合力也是恒力,小球将沿合力方向做匀加速直线运动.根据牛顿第二定律求出加速度.
解答 解:(1)小球静止在电场中受力如图所示 :
:
显然小球带正电,由平衡条件得:
mgtan37°=qE
故E=$\frac{3mg}{4q}$.小球带正电.
(2)丝线剪断后,小球由静止沿丝线的反方向作匀加速直线运动,可把此运动分解为水平方向的匀加速直线运动和竖直方向的自由落体运动:研究竖直自由落体运动;
剪断丝线后,小球受到重力、电场力作用,小球将沿两个力的合力方向做匀加速直线运动.有:
F合=$\frac{mg}{cos37°}$=$\frac{5mg}{4}$
根据牛顿第二定律得:F合=ma
则有:a=$\frac{5}{4}$g
又有:$\frac{2L-Lcos37°}{cos37°}$=$\frac{1}{2}$at2
得:t=$\sqrt{\frac{3L}{g}}$
答:(1)小球带正电及匀强电场的电场强度的大小$\frac{3mg}{4q}$;
(2)若剪断丝线,小球将将沿两个力的合力方向做匀加速直线运动,小球从剪断丝线开始到到达地面经过的时间$\sqrt{\frac{3L}{g}}$.
点评 本题是带电粒子在电场中平衡和匀变速运动问题,关键是分析受力情况和运动情况,用动力学基本的方法处理.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
20. 如图所示,长方体物块A叠放在长方体物块B上,B置于粗糙水平面上.A、B质量分别为mA=2kg,mB=1kg,A、B之间动摩擦因数μ1=0.2,B与地面之间动摩擦因数μ2=0.1,现对A施加水平力F,若F从0 开始逐渐增加,则( )
如图所示,长方体物块A叠放在长方体物块B上,B置于粗糙水平面上.A、B质量分别为mA=2kg,mB=1kg,A、B之间动摩擦因数μ1=0.2,B与地面之间动摩擦因数μ2=0.1,现对A施加水平力F,若F从0 开始逐渐增加,则( )
 如图所示,长方体物块A叠放在长方体物块B上,B置于粗糙水平面上.A、B质量分别为mA=2kg,mB=1kg,A、B之间动摩擦因数μ1=0.2,B与地面之间动摩擦因数μ2=0.1,现对A施加水平力F,若F从0 开始逐渐增加,则( )
如图所示,长方体物块A叠放在长方体物块B上,B置于粗糙水平面上.A、B质量分别为mA=2kg,mB=1kg,A、B之间动摩擦因数μ1=0.2,B与地面之间动摩擦因数μ2=0.1,现对A施加水平力F,若F从0 开始逐渐增加,则( )| A. | 当拉力小于3N时,A、B 都相对地面静止 | |
| B. | 当拉力超过4 N时,A、B开始发生相对滑动 | |
| C. | 当拉力超过5 N时,B的加速度为1m/s2 | |
| D. | 当拉力超过6 N时,A、B开始发生相对滑动 |
7.质量为1kg的小球从高20m处自由下落到软垫上,反弹后上升的最大高度为5m,小球接触软垫的时间是1s.在接触时间内,小球受到的平均冲力大小为(空气阻力不计,g=10m/s2)( )
| A. | 10N | B. | 20N | C. | 30N | D. | 40N |
17. 如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2r,rB=r,若皮带不打滑,则下列说法正确的是( )
如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2r,rB=r,若皮带不打滑,则下列说法正确的是( )
 如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2r,rB=r,若皮带不打滑,则下列说法正确的是( )
如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2r,rB=r,若皮带不打滑,则下列说法正确的是( )| A. | a点与b点的线速度大小相等 | B. | a点与b点的角速度大小相等 | ||
| C. | a点与c点的线速度大小相等 | D. | b点与c点的向心加速度大小相等 |
1.设行星a和行星b是两个均匀球体,两行星的质量之比ma:mb=2:1,半径之比Ra:Rb=1:2.行星a的卫星绕其表面附近做圆周运动的周期为Ta,行星b的卫星绕其表面附近做圆周运动的周期为Tb,则它们的周期之比Ta:Tb为( )
| A. | 1:4 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
8. 如图所示,在垂直于纸面向里的匀强磁场中,从P点垂直于磁场方向发射两个电子1和2,其速度分别为v1和v2,如果v2=2v1,则1和2电子的轨道半径之比r1:r2及周期之比T1:T2分别为( )
如图所示,在垂直于纸面向里的匀强磁场中,从P点垂直于磁场方向发射两个电子1和2,其速度分别为v1和v2,如果v2=2v1,则1和2电子的轨道半径之比r1:r2及周期之比T1:T2分别为( )
 如图所示,在垂直于纸面向里的匀强磁场中,从P点垂直于磁场方向发射两个电子1和2,其速度分别为v1和v2,如果v2=2v1,则1和2电子的轨道半径之比r1:r2及周期之比T1:T2分别为( )
如图所示,在垂直于纸面向里的匀强磁场中,从P点垂直于磁场方向发射两个电子1和2,其速度分别为v1和v2,如果v2=2v1,则1和2电子的轨道半径之比r1:r2及周期之比T1:T2分别为( )| A. | r1:r2=1:2 T1:T2=1:2 | B. | r1:r2=1:2 T1:T2=1:1 | ||
| C. | r1:r2=2:1 T1:T2=1:1 | D. | r1:r2=2:1 T1:T2=2:1 |

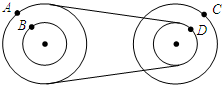 两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2:1,CD两点的半径之比也为2:1,则ABCD四点的角速度之比为1:1:2:2,这四点的线速度之比为2:1:4:2,向心加速度之比为2:1:8:4.
两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2:1,CD两点的半径之比也为2:1,则ABCD四点的角速度之比为1:1:2:2,这四点的线速度之比为2:1:4:2,向心加速度之比为2:1:8:4.