题目内容
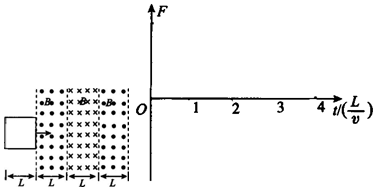
13.长木板A放在光滑的水平面上,质量为m=4kg的物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,A、B速度随时间变化情况如图所示,则下列说法正确的是( )
| A. | 木板获得的动能为2J | B. | 系统损失的机械能为6J | ||
| C. | 木板A的最小长度为2m | D. | A、B间的动摩擦因数为0.2 |
分析 根据v-t图象可得到木板获得的速度,根据动量守恒定律求出A的质量,从而求得木板获得的动能和系统损失的机械能,根据图象的斜率得出两物体的加速度,根据牛顿第二定律求解即可A、B间的动摩擦因数.根据速度图象与时间轴所围的“面积”求出B相对于A滑行的位移,即可得到木板A的最小长度.
解答 解:A、从图2可以看出,B先做匀减速运动,A先做匀加速运动,最后一起做匀速运动,共同速度 v=1m/s.
取向右为正方向,根据动量守恒定律得 mv0=(m+mA)v,解得 mA=4kg
木板获得的动能为 EkA=$\frac{1}{2}$mAv2=$\frac{1}{2}×4×{1}^{2}$=2J,故A正确;
B、系统损失的机械能△E=$\frac{1}{2}$mv02-$\frac{1}{2}$(mA+m)2=$\frac{1}{2}$×4×22-$\frac{1}{2}$×8×12=4J,故B错误;
C、由图象可知1s内物体B的位移为 xB=$\frac{2+1}{2}$×1m=1.5m,木板A的位移为 xA=$\frac{1}{2}$×1×1m=0.5m,所以木板最小长度为 L=xB-xA=1m,故C错误;
D、由图象可知木板A的加速度为 aA=$\frac{v}{t}$=$\frac{1}{1}$=1m/s2,根据μmg=mAaA得出动摩擦因数为0.1,故D错误.
故选:A
点评 解决本题的关键是要明确B在A上滑行时系统遵守动量守恒定律.要知道v-t图象的斜率等于加速度,“面积”表示位移.

练习册系列答案
相关题目
3.弹簧振子在振动过程中,振子经a、b两点的速度相等,且从a点运动到b点最短历时为0.2s,从b点再到b点最短历时0.2s,则这个弹簧振子的振动周期和频率分别为( )
| A. | 0.4s,2.5Hz | B. | 0.8s,2.5Hz | C. | 0.4s,1.25Hz | D. | 0.8s,1.25Hz |
4.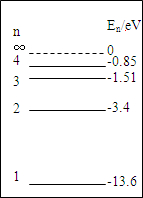 如图所示为氢原子能级示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干种不同频率的光子.下列说法正确的是( )
如图所示为氢原子能级示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干种不同频率的光子.下列说法正确的是( )
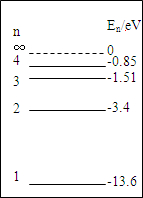 如图所示为氢原子能级示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干种不同频率的光子.下列说法正确的是( )
如图所示为氢原子能级示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干种不同频率的光子.下列说法正确的是( )| A. | 这些氢原子总共可辐射出3种不同频率的光子 | |
| B. | 由n=4能级跃迁到n=1能级产生的光波长最短 | |
| C. | 由n=2能级跃迁到n=1能级产生的光频率最小 | |
| D. | 用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34eV的金属铂不能发生光电效应 |
1. 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )| A. | 两小球机械能均逐渐减小 | B. | 两小球机械能总是相等的 | ||
| C. | 两小球经最低点时动能相等 | D. | 两小球到最低点时重力做功相等 |
8.据中央气象台消息:
2017年第1号台风“梅花(Muifa)”于4月26日在距离菲律宾马尼拉以东方向1640公里的西北太平洋海面上生成(东经136.1°,北纬13.4°),中心附近最大风速18m/s(8级风,热带风暴级).预计“梅花”将以12km/h左右的速度向西北方向移动,强度变化不大.
关于上述消息中的“18m/s、12km/h”,下述理解中正确的是( )
2017年第1号台风“梅花(Muifa)”于4月26日在距离菲律宾马尼拉以东方向1640公里的西北太平洋海面上生成(东经136.1°,北纬13.4°),中心附近最大风速18m/s(8级风,热带风暴级).预计“梅花”将以12km/h左右的速度向西北方向移动,强度变化不大.
关于上述消息中的“18m/s、12km/h”,下述理解中正确的是( )
| A. | 分别指平均速度和瞬时速度的大小 | B. | 分别指瞬时速度和平均速度的大小 | ||
| C. | 均指平均速度的大小 | D. | 均指瞬时速度的大小 |
18. 如图所示,倾斜角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏相连,连接b的一段细线与斜面平行.在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
如图所示,倾斜角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏相连,连接b的一段细线与斜面平行.在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
 如图所示,倾斜角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏相连,连接b的一段细线与斜面平行.在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
如图所示,倾斜角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏相连,连接b的一段细线与斜面平行.在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )| A. | b对c的摩擦力一定减小 | |
| B. | b对c的摩擦力方向可能平行于斜面向上 | |
| C. | 地面对c的摩擦力方向一定向左 | |
| D. | 地面对c的摩擦力一定减小 |
20.对开普勒第三定律$\frac{{a}^{3}}{{T}^{2}}$=k,以下理解正确的是( )
| A. | a代表行星运动的轨道半径 | B. | k是一个与行星有关的常量 | ||
| C. | T代表行星运动的自转周期 | D. | T代表行星运动的公转周期 |
 如图所示,x轴上放有一足够大的荧光屏,y轴上(0,L)处有一个点状的α粒子放射源A,某瞬间同时向xOy平面内各个方向发射速率均为v0的α粒子(不计重力),设α粒子电量为q,质量为m.求:
如图所示,x轴上放有一足够大的荧光屏,y轴上(0,L)处有一个点状的α粒子放射源A,某瞬间同时向xOy平面内各个方向发射速率均为v0的α粒子(不计重力),设α粒子电量为q,质量为m.求: