题目内容
4.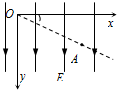 如图所示,竖直平面内存在竖直向下的匀强电场,质量为m的带正电小球以速度v从O点沿O x轴水平射入,且恰好能通过A点,OA与x轴成300角,则小球通过A点时的动能为$\frac{7}{6}$mv2.
如图所示,竖直平面内存在竖直向下的匀强电场,质量为m的带正电小球以速度v从O点沿O x轴水平射入,且恰好能通过A点,OA与x轴成300角,则小球通过A点时的动能为$\frac{7}{6}$mv2.
分析 小球在电场中受到重力和电场力而做类平抛运动,水平方向不受力做匀速运动,运用速度合成,求出P点的速度,再求出动能.
解答 解:小球做类平抛运动,位移偏向角为:
tan30°=$\frac{y}{x}$=$\frac{\frac{1}{2}a{t}^{2}}{{v}_{0}t}$=$\frac{at}{2{v}_{0}}$=$\frac{{v}_{y}}{2{v}_{0}}$,
得:vy=$\frac{2\sqrt{3}}{3}{v}_{0}$,
故在A点的动能为:
EK=$\frac{1}{2}$mv′2=$\frac{1}{2}$m(v2+vy2)=$\frac{7}{6}$mv2.
故答案为:$\frac{7}{6}$mv2
点评 本题考查带电粒子在电场中的运动规律的分析,主要考查灵活选择解题规律的能力.类平抛运动通常用动力学方法处理,注意OA连线为小球通过的位移,所以根据位移公式进行分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,在O点固定一负点电荷,实线为其中几条对称分布的电场线,虚线为以Oe电场线上的O′点为圆心的一个圆,a、b、c、d、e,f、g、h为圆与电场线的交点,下列说法正确的是( )
如图所示,在O点固定一负点电荷,实线为其中几条对称分布的电场线,虚线为以Oe电场线上的O′点为圆心的一个圆,a、b、c、d、e,f、g、h为圆与电场线的交点,下列说法正确的是( )
 如图所示,在O点固定一负点电荷,实线为其中几条对称分布的电场线,虚线为以Oe电场线上的O′点为圆心的一个圆,a、b、c、d、e,f、g、h为圆与电场线的交点,下列说法正确的是( )
如图所示,在O点固定一负点电荷,实线为其中几条对称分布的电场线,虚线为以Oe电场线上的O′点为圆心的一个圆,a、b、c、d、e,f、g、h为圆与电场线的交点,下列说法正确的是( )| A. | b、h两点的电场强度相同 | |
| B. | a点电势比e点电势高 | |
| C. | d、b两点间电势差大于e、b两点间电势差 | |
| D. | 将电子沿圆周由h运动到d与由h运动到f,电场力做功相等 |
9. 如图,某带电粒子由静止开始经电压为 U 的电场加速后,射入水平放置、电势差为 U′的两导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁感线方向射入边界线竖直的匀强磁场中,则粒子进入磁场和射出磁场的 M,N 两点间的距离 d 随着 U 和 U′的变化情况为(不计重力,不考虑边缘效应)( )
如图,某带电粒子由静止开始经电压为 U 的电场加速后,射入水平放置、电势差为 U′的两导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁感线方向射入边界线竖直的匀强磁场中,则粒子进入磁场和射出磁场的 M,N 两点间的距离 d 随着 U 和 U′的变化情况为(不计重力,不考虑边缘效应)( )
 如图,某带电粒子由静止开始经电压为 U 的电场加速后,射入水平放置、电势差为 U′的两导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁感线方向射入边界线竖直的匀强磁场中,则粒子进入磁场和射出磁场的 M,N 两点间的距离 d 随着 U 和 U′的变化情况为(不计重力,不考虑边缘效应)( )
如图,某带电粒子由静止开始经电压为 U 的电场加速后,射入水平放置、电势差为 U′的两导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁感线方向射入边界线竖直的匀强磁场中,则粒子进入磁场和射出磁场的 M,N 两点间的距离 d 随着 U 和 U′的变化情况为(不计重力,不考虑边缘效应)( )| A. | d 随 U 变化,d 随 U′变化 | B. | d 随 U 变化,d 与 U′无关 | ||
| C. | d 与 U 无关,d 与 U′无关 | D. | d 与 U 无关,d 随 U′变化 |
16.示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成,如图所示.如果在荧光屏上P点出现亮斑(亮斑图是从右向左看屏),那么示波管中的( )


| A. | 极板X应带负电 | B. | 极板X'应带负电 | C. | 极板Y应带正电 | D. | 极板Y'应带正电 |
14. 如图所示,质量m=1kg的带电滑块与水平面间的动摩擦因数μ=0.1,由于空间存在水平方向的匀强电场,因此滑块还受到大小为5N、方向水平向右的电场力 F 的作用,则滑块在向左运动的过程中所受的摩擦力(取重力加速度g=10m/s2)( )
如图所示,质量m=1kg的带电滑块与水平面间的动摩擦因数μ=0.1,由于空间存在水平方向的匀强电场,因此滑块还受到大小为5N、方向水平向右的电场力 F 的作用,则滑块在向左运动的过程中所受的摩擦力(取重力加速度g=10m/s2)( )
 如图所示,质量m=1kg的带电滑块与水平面间的动摩擦因数μ=0.1,由于空间存在水平方向的匀强电场,因此滑块还受到大小为5N、方向水平向右的电场力 F 的作用,则滑块在向左运动的过程中所受的摩擦力(取重力加速度g=10m/s2)( )
如图所示,质量m=1kg的带电滑块与水平面间的动摩擦因数μ=0.1,由于空间存在水平方向的匀强电场,因此滑块还受到大小为5N、方向水平向右的电场力 F 的作用,则滑块在向左运动的过程中所受的摩擦力(取重力加速度g=10m/s2)( )| A. | 大小为5N,方向水平向右 | B. | 大小为5N,方向水平向左 | ||
| C. | 大小为1N,方向水平向右 | D. | 大小为1N,方向水平向左 |
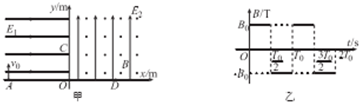 在竖直平面内的直角坐标系xOy,x轴沿水平方向,如图甲所示,第二象限内有一水平向右的匀强电场,场强为E1,坐标系的第一象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{{E}_{1}}{2}$匀强磁场方向垂直纸面,一个质重m=0.01g、带电荷量9=+1.0×10-3C的微粒以v0=4m/s的速度垂直x轴从A点竖直向上射入第二象限,随后又以v1=8m/s的速度从+y轴上的C点沿水平方向进入第一象限,取微粒刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),重力加速度月取10m/s2.求:
在竖直平面内的直角坐标系xOy,x轴沿水平方向,如图甲所示,第二象限内有一水平向右的匀强电场,场强为E1,坐标系的第一象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{{E}_{1}}{2}$匀强磁场方向垂直纸面,一个质重m=0.01g、带电荷量9=+1.0×10-3C的微粒以v0=4m/s的速度垂直x轴从A点竖直向上射入第二象限,随后又以v1=8m/s的速度从+y轴上的C点沿水平方向进入第一象限,取微粒刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),重力加速度月取10m/s2.求: 如图所示,粒子源S不断地产生质量为m、电量为+q的粒子(重力不计),粒子从O1孔进入一个电压为U的加速电场,经小孔O2从中央水平射入方向垂直于纸面向里,磁感强度为B的正方形匀强磁场区域,粒子进入小孔O1的初速度为零,求:
如图所示,粒子源S不断地产生质量为m、电量为+q的粒子(重力不计),粒子从O1孔进入一个电压为U的加速电场,经小孔O2从中央水平射入方向垂直于纸面向里,磁感强度为B的正方形匀强磁场区域,粒子进入小孔O1的初速度为零,求: 如图,一粒子发射源P位于足够大绝缘板A的上方d处,能够在纸面内向各个方向发射速率为v、电荷量为q、质量为m的带正电的粒子,空间存在垂直纸面的匀强磁场,不考虑粒子间的相互作用和粒子重力,已知粒子做圆周运动的半径大小恰好为d,求:
如图,一粒子发射源P位于足够大绝缘板A的上方d处,能够在纸面内向各个方向发射速率为v、电荷量为q、质量为m的带正电的粒子,空间存在垂直纸面的匀强磁场,不考虑粒子间的相互作用和粒子重力,已知粒子做圆周运动的半径大小恰好为d,求: 如图所示,截面为直角三角形的木块置于粗糙的水平地面上,其倾角30°.现有一质量m=l.0kg的滑块从斜面下滑,测得滑块在起动后的0.40s沿斜面运动了0.32m,且知滑块滑行过程中木块处于静止状态,重力加速度g=10m/s2,求:
如图所示,截面为直角三角形的木块置于粗糙的水平地面上,其倾角30°.现有一质量m=l.0kg的滑块从斜面下滑,测得滑块在起动后的0.40s沿斜面运动了0.32m,且知滑块滑行过程中木块处于静止状态,重力加速度g=10m/s2,求: