题目内容
20. 如图所示,在竖直方向的磁感应强度为B的匀强磁场中,金属框架OACBD固定在水平面内,OA与OB的夹角为60°,OA、OB、MN三根导体棒的长度均为1,它们单位长度的电阻为r,其他部分的电阻不计.MN在外力的作用下以垂直于自身的速度v向右匀速运动,导体棒在滑动的过程中始终保持与导轨良好的接触,经过O点瞬间作为计时起点.(已知B=0.2T,l=0.5m,r=0.1Ω,v=0.3m/s)
如图所示,在竖直方向的磁感应强度为B的匀强磁场中,金属框架OACBD固定在水平面内,OA与OB的夹角为60°,OA、OB、MN三根导体棒的长度均为1,它们单位长度的电阻为r,其他部分的电阻不计.MN在外力的作用下以垂直于自身的速度v向右匀速运动,导体棒在滑动的过程中始终保持与导轨良好的接触,经过O点瞬间作为计时起点.(已知B=0.2T,l=0.5m,r=0.1Ω,v=0.3m/s)(1)导体棒滑到AB时,流过MN的电流的大小和方向;
(2)导体棒滑到AB之前的t时刻,整个电路的电功率是多少?
(3)0.2秒内产生的系统产生的焦耳热?
分析 (1)导体棒滑到AB时,由右手定则判断感应电流的方向.由E=Blv求出MN产生的感应电动势,分析回路的总电阻,再求电流.
(2)根据几何关系写出有效长度与时间的表达式,然后根据法拉第电磁感应定律求得感应电动势,再由功率公式求解.
(3)由能量守恒定律求出焦耳热.
解答 解:(1)导体棒滑到AB时,由右手定则判断知,流过MN的电流方向由N→M.
MN产生的感应电动势为:E=Blv=0.2×0.5×0.3V=0.03V
回路的总电阻为:R=3lr=3×0.5×0.1=0.15Ω
电流为:I=$\frac{E}{R}$=0.2A
(2)导体棒滑到AB之前的t时刻,有效切割长度为:L=2vt•tan30°
回路的总电阻为:Rt=3Lr
感应电动势为:Et=BLv
回路中感应电流为:I=$\frac{{E}_{t}}{{R}_{t}}$=$\frac{Bv}{3r}$=0.2A
整个电路的电功率是:P=$\frac{{E}_{t}^{2}}{{R}_{t}}$
联立解得:P=0.0024$\sqrt{3}$t W
(3)0.2s内棒MN移动的距离为:x=vt=0.06m
此时棒受到的安培力大小为:F=BI•2xtan30°=0.0016$\sqrt{3}$ N
克服安培力做功为:W=$\frac{F}{2}$x=4.8$\sqrt{3}×1{0}^{-5}$J
根据能量守恒定律知,系统产生的焦耳热为:Q=W=4.8$\sqrt{3}×1{0}^{-5}$J
答:(1)导体棒滑到AB时,流过MN的电流的大小是0.2A,方向由N→M;
(2)导体棒滑到AB之前的t时刻,整个电路的电功率是0.0024$\sqrt{3}$tW.
(3)0.2秒内产生的系统产生的焦耳热是4.8$\sqrt{3}×1{0}^{-5}$J.
点评 解决本题关键是确定导体棒有效的切割长度,即导体棒与导轨两个交点间的距离,掌握切割感应电动势公式和运动学公式,并能结合解题.

 阅读快车系列答案
阅读快车系列答案 甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图象中(如图),直线a、b分别描述了甲、乙两车在0~20s的运动情况.关于两车之间的位移关系,下列说法正确的是( )
甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图象中(如图),直线a、b分别描述了甲、乙两车在0~20s的运动情况.关于两车之间的位移关系,下列说法正确的是( )| A. | 在0~10 s内两车逐渐远离 | |
| B. | 在10~20 s内两车逐渐远离 | |
| C. | 在5s和15 s时刻,两车的间距不相等 | |
| D. | 在t=20 s时两车在公路上相遇 |
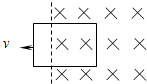 如图所示,先后以速度v1和v2(v1=2v2),匀速地把同一线圈从同一位置拉出有界匀强磁场的过程中,在先后两种情况下,以下错误的是( )
如图所示,先后以速度v1和v2(v1=2v2),匀速地把同一线圈从同一位置拉出有界匀强磁场的过程中,在先后两种情况下,以下错误的是( )| A. | 线圈的感应电流大小之比为1:2 | |
| B. | 线圈产生的热量之比为1:2 | |
| C. | 通过导体截面的电量之比为1:2 | |
| D. | 沿运动方向作用在线圈上的外力的功率之比为1:4 |
| U(V) | 1.37 | 1.32 | 1.24 | 1.18 | 1.10 | 1.05 |
| I(A) | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
| A. | 有核能释放的核反应一定有质量亏损 | |
| B. | 由波尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减少,电势能增大 | |
| C. | α粒子散射实验中少数α粒子发生了较大偏转,这是卢瑟福猜想原子核式结构模型的主要依据之一 | |
| D. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此光子散射后频率变大 |
 如图甲所示,某同学利用光电计时器等器材验证机械能守恒定律.用游标卡尺测得金属小球的直径为d,小球由A处静止释放,通过A处正下方、固定于B处的光电门,光电计时器记录下小球通过光电门的时间为r,测得A、B间的高度为H(H》d),多次改变高度H,重复上述实验操作,得到多个H及对应的t.当地重力加速度为g.
如图甲所示,某同学利用光电计时器等器材验证机械能守恒定律.用游标卡尺测得金属小球的直径为d,小球由A处静止释放,通过A处正下方、固定于B处的光电门,光电计时器记录下小球通过光电门的时间为r,测得A、B间的高度为H(H》d),多次改变高度H,重复上述实验操作,得到多个H及对应的t.当地重力加速度为g. 如图所示,一横截面为扇形ABC的玻璃砖放置在水平面上,∠ABC=75°,扇形半径R=AB=BC=10cm,一束水平光线以45°入射角射到弧面AC点,玻璃对光的折射率为$\sqrt{2}$,求:
如图所示,一横截面为扇形ABC的玻璃砖放置在水平面上,∠ABC=75°,扇形半径R=AB=BC=10cm,一束水平光线以45°入射角射到弧面AC点,玻璃对光的折射率为$\sqrt{2}$,求:
