题目内容
13. 如图所示,有一与液面成45°角的光线从透明液体射向空中,光源距离液面高度为1m,离开该液体表面的光线与液面的夹角为30°.试求:
如图所示,有一与液面成45°角的光线从透明液体射向空中,光源距离液面高度为1m,离开该液体表面的光线与液面的夹角为30°.试求:①该液体的折射率;
②这束光线经多长时间可以从光源到达液面;
③如果要使空中没有折射光线出现,入射光线需要与地面成多大的角度.
分析 ①由图得到入射角和折射角,由折射定律求液体的折射率;
②由几何关系求出光在液体中传播的距离,由v=$\frac{c}{n}$求光在液体中传播的速度,即可求得传播时间.
③如果要使空中没有折射光线出现,光线在液面发生全反射,由sinC=$\frac{1}{n}$求出临界角,再由几何知识求解.
解答 解:①由图得:入射角 i=45°,折射角 r=60°
根据折射定律,有 n=$\frac{sinr}{sini}$=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{2}$
②由几何关系,得光在液体中传播的距离为
S=$\sqrt{2}$m
光在液体中传播的速度 v=$\frac{c}{n}$
则这束光线从光源到达液面传播时间 t=$\frac{S}{v}$=$\frac{nS}{c}$=$\frac{\frac{\sqrt{6}}{2}×\sqrt{2}}{3×1{0}^{8}}$=$\sqrt{3}$×10-8s
②设发生全发射的临界角为C,则
sinC=$\frac{1}{n}$=$\frac{\sqrt{6}}{3}$
解得 C=arcsin$\frac{\sqrt{6}}{3}$
所以如果要使空中没有折射光线出现,入射光线需要与地面成arcsin$\frac{\sqrt{6}}{3}$的角度.
答:
①该液体的折射率是$\frac{\sqrt{6}}{2}$;
②这束光线经$\sqrt{3}$×10-8s时间可以从光源到达液面;
③如果要使空中没有折射光线出现,入射光线需要与地面成arcsin$\frac{\sqrt{6}}{3}$的角度.
点评 本题是几何光学中基本问题,要掌握折射定律和光速公式,运用几何知识求入射角和折射角.要注意公式n=$\frac{sini}{sinr}$适用的前提条件是光从真空射入介质折射.

 名校课堂系列答案
名校课堂系列答案| A. | 1:1 | B. | 1:4 | C. | 4:1 | D. | 2:1 |
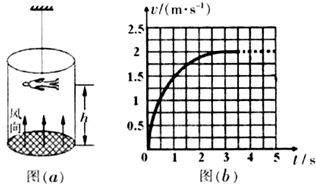
①安装实验器材,调节试管夹(小铁球)、光电门和纸杯在同一竖直线上;
②打开试管夹,由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t,并用刻度尺(图上未画出)测量出两个光电门之间的高度h,计算出小铁球通过两光电门间的平均速度v;
③保持光电门1的位置不变,改变光电门2的位置,重复②的操作.测出多组(h,t),计算出对应的平均速度v;

④画出v-t图象.
请根据实验,回答如下问题:
(1)设小铁球到达光电门1时的速度为v0,当地的重力加速度为g.则小铁球通过两光电门间平均速度v的表达式为v=v0+$\frac{1}{2}$gt.(用v0、g和t表示)
(2)实验测得的数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| h(cm) | 10.00 | 20.00 | 30.00 | 40.00 | 50.00 | 60.00 |
| t(s) | 0.069 | 0.119 | 0.159 | 0.195 | 0.226 | 0.255 |
| v(m•S-1) | 1.45 | 1.68 | 1.89 | 2.05 | 2.21 | 2.35 |
(3)根据v-t图象,可以求得当地重力加速度g=9.7m/s2,试管夹到光电门1的距离约为6.2 cm.(以上结果均保留两位有效数字)
| A. | 在滑跑过程中飞机的加速度大小为3.6m/s2 | |
| B. | 飞机在滑跑过程中,发动机的功率恒定 | |
| C. | 在滑跑过程中牵引力对飞机做功的平均功率为5.7×105W | |
| D. | 比例系数k=$\frac{125}{9}$N•s2•m-2 |
 如图,位于水平面的圆盘绕过圆心O的竖直转轴做圆周运动,在圆盘上有一质量为m的小木块,距圆心的距离为r,木块与圆盘间的最大静摩擦力为压力的k倍,在圆盘转速缓慢增大的过程中,下列说法正确的是( )
如图,位于水平面的圆盘绕过圆心O的竖直转轴做圆周运动,在圆盘上有一质量为m的小木块,距圆心的距离为r,木块与圆盘间的最大静摩擦力为压力的k倍,在圆盘转速缓慢增大的过程中,下列说法正确的是( )| A. | 摩擦力对小木块做正功,其机械能增加 | |
| B. | 小木块获得的最大动能为$\frac{1}{4}$kmgr | |
| C. | 小木块所受摩擦力提供向心力,始终指向圆心,故不对其做功 | |
| D. | 小木块受重力、支持力和向心力 |
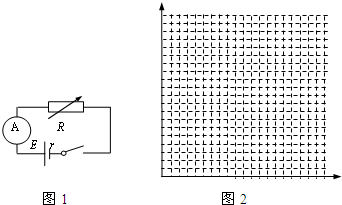
| 次数 | 1 | 2 | 3 | 4 | 5 |
| R(Ω) | 4.0 | 10.0 | 16.0 | 22.0 | 28.0 |
| I(A) | 1.00 | 0.50 | 0.34 | 0.25 | 0.20 |
| $\frac{1}{I}$(A-1) | 1.0 | 2.0 | 2.9 | 4.0 | 5.0 |
(2)利用测得的数据在图2中的坐标纸上画出适当的图象;
(3)由图象可知,该电池的电动势E=6V,内阻r=2.0Ω.