题目内容
14. 如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( )
如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( )| A. | 在竖直位置两球的速度大小均为$\sqrt{2gL}$ | |
| B. | 杆竖直位置时对m球的作用力向上,大小为$\frac{1}{3}$mg | |
| C. | 杆竖直位置时铁钉对杆的作用力为0 | |
| D. | 由于忽略一切摩擦阻力,根据机械能守恒,杆一定能绕铁钉做完整的圆周运动 |
分析 将轻杆从水平位置由静止释放,转到竖直位置时,A、B两球的速度大小相等,根据系统的机械能守恒,求出速度大小.对B研究,根据牛顿第二定律求解杆的作用力大小和方向,分析机械能的变化,判断A的机械能是否守恒.
解答 解:A、将轻杆从水平位置由静止释放,转到竖直位置时,两球的速度大小相等,设为v,根据系统的机械能守恒,得
2mgL-mgL=$\frac{1}{2}$•3mv2,解得,v=$\sqrt{\frac{2}{3}gL}$.故A错误.
B、杆转到竖直位置时,对m球:mg-N=m$\frac{{v}^{2}}{L}$,解得,N=$\frac{1}{3}$mg,故B正确.
C、杆转到竖直位置时,对2m球:N′-2mg=2m$\frac{{v}^{2}}{L}$,解得,N′=$\frac{10}{3}$mg,所以铁钉对杆的作用力向上,大小为N+N′=$\frac{11}{3}$mg,故C错误;
D、由机械能守恒定律分析得知,当系统顺时针转到水平位置时速度为零,然后再逆时针转动,不可能做完整的圆周运动.故D错误.
故选:B.
点评 本题是轻杆连接的模型问题,对系统机械能是守恒的,但对单个小球机械能并不守恒,运用系统机械能守恒和牛顿运动定律结合研究.

练习册系列答案
相关题目
2. 如图所示,竖直放置的条形磁铁中央,有一闭合金属弹性圆环,条形磁铁中心线与弹性环轴线重合,现将弹性圆环均匀向外扩大,下列说法中正确的是( )
如图所示,竖直放置的条形磁铁中央,有一闭合金属弹性圆环,条形磁铁中心线与弹性环轴线重合,现将弹性圆环均匀向外扩大,下列说法中正确的是( )
 如图所示,竖直放置的条形磁铁中央,有一闭合金属弹性圆环,条形磁铁中心线与弹性环轴线重合,现将弹性圆环均匀向外扩大,下列说法中正确的是( )
如图所示,竖直放置的条形磁铁中央,有一闭合金属弹性圆环,条形磁铁中心线与弹性环轴线重合,现将弹性圆环均匀向外扩大,下列说法中正确的是( )| A. | 穿过弹性圆环的磁通量增大 | |
| B. | 从上往下看,弹性圆环中有顺时针方向的感应电流 | |
| C. | 弹性圆环中无感应电流 | |
| D. | 弹性圆环受到的安培力方向沿半径向里 |
19. 匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°∠c=90°,bc的长度为1cm.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.则( )
匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°∠c=90°,bc的长度为1cm.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.则( )
 匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°∠c=90°,bc的长度为1cm.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.则( )
匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°∠c=90°,bc的长度为1cm.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.则( )| A. | 该三角形的内切圆上最高电势为3V | |
| B. | 该三角形的内切圆上最低电势为0V | |
| C. | 该匀强电场电场强度大小为100$\sqrt{3}$V/m | |
| D. | 该匀强电场电场强度大小为400V/m |




 如图所示,一质点以初速度v0正对着倾角θ=37°,的斜面水平抛出,空气阻力不计,重力加速度为g,sin37°=0.6,cos37°=0.8,要求质点到达斜面过程很位移最小,求质点在空中飞行的时间t.
如图所示,一质点以初速度v0正对着倾角θ=37°,的斜面水平抛出,空气阻力不计,重力加速度为g,sin37°=0.6,cos37°=0.8,要求质点到达斜面过程很位移最小,求质点在空中飞行的时间t.
 如图所示,物体静止在水平桌面上.图中用于表示物体对桌面的压力是F3.(填“F1”、“F2”或“F3”)
如图所示,物体静止在水平桌面上.图中用于表示物体对桌面的压力是F3.(填“F1”、“F2”或“F3”)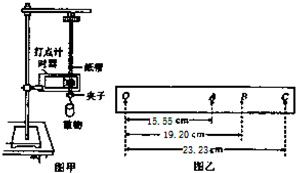 用如图甲所示的实验装置验证机械能守恒定律,质量m=100g的重物拖动纸带自由下落,打点计时器在纸带上打出一系列点.如图乙所示为选取的一条符合实验要求的纸带,O 点为打出的第一个点,A、B、C为从合适位置开始选取的三个连续的点(其它点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么:
用如图甲所示的实验装置验证机械能守恒定律,质量m=100g的重物拖动纸带自由下落,打点计时器在纸带上打出一系列点.如图乙所示为选取的一条符合实验要求的纸带,O 点为打出的第一个点,A、B、C为从合适位置开始选取的三个连续的点(其它点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么: 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s.
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s.