题目内容
9. 如图所示,相距为d的两条水平虚线之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方h高处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度为v0,则线圈穿过磁场的过程中(从cd边刚进入磁场起一直到ab边离开磁场为止)( )
如图所示,相距为d的两条水平虚线之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方h高处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度为v0,则线圈穿过磁场的过程中(从cd边刚进入磁场起一直到ab边离开磁场为止)( )| A. | 线框穿过磁场的过程先减速后加速 | |
| B. | 安培力所做的功为mg(d+L) | |
| C. | 线圈的最小速度一定是$\sqrt{2g(h+L-d)}$ | |
| D. | 线圈进入磁场和穿出磁场的过程比较,所用时间不一样 |
分析 线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时刻的速度是相同的,又因为线圈全部进入磁场不受安培力,要做匀加速运动.可知线圈进入磁场先要做减速运动.根据线框的运动情况,分析进入和穿出磁场的时间关系.根据动能定理求出安培力做功的大小,当线框全部进入磁场的瞬间,速度最小,根据动能定理求出最小速度.
解答 解:A、cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度为v0,因为线框全部进入磁场后做加速运动,可知线框进入磁场时做减速,全部进入磁场后做加速,出磁场时做减速,故A错误.
B、从cd边刚进入磁场到cd边刚离开磁场的过程,根据动能定理得:mgd+WA=0,解得安培力做功为:WA=-mgd,出磁场的过程和进入磁场的过程相同,可知整个过程安培力做功为-2mgd,故B错误.
C、全部进入磁场的瞬间速度最小,从cd边刚进入磁场到线框完全进入时,则有:$mgL+{W}_{A}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,又$mgh=\frac{1}{2}m{{v}_{0}}^{2}$,解得最小速度为:v=$\sqrt{2g(h+L-d)}$,故C正确.
D、cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,故知线圈进入磁场和穿出磁场的过程运动情况相同,所用的时间一样,故D错误.
故选:C.
点评 解决本题的关键根据根据线圈下边缘刚进入磁场和刚穿出磁场时刻的速度都是v0,且全部进入磁场将做加速运动,判断出线圈进磁场后先做变减速运动,也得出全部进磁场时的速度是穿越磁场过程中的最小速度.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
8.下面给出的电磁波中,是由原子内层电子受激后产生的( )
| A. | 伦琴(X)射线 | B. | 红外线 | C. | 无线电波 | D. | 紫外线 |
20.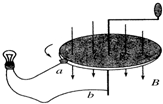 如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中有大小和方向作周期性变化的电流 | |
| B. | 回路中电流大小恒定,且等于$\frac{{B{L^2}ω}}{2R}$ | |
| C. | 回路中电流方向不变,且从b导线流进灯泡,再从a导线流向旋转的铜盘 | |
| D. | 回路中电流方向不变.且从α导线流进灯泡.再从b导线流向旋转的铜盘 |
17. 我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,“天链一号”卫星a、赤道平面内的低轨道卫星b,地球的位置关系如图所示,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,且均绕地球同向运行,已知卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略,下列分析正确的是( )
我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,“天链一号”卫星a、赤道平面内的低轨道卫星b,地球的位置关系如图所示,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,且均绕地球同向运行,已知卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略,下列分析正确的是( )
 我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,“天链一号”卫星a、赤道平面内的低轨道卫星b,地球的位置关系如图所示,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,且均绕地球同向运行,已知卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略,下列分析正确的是( )
我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,“天链一号”卫星a、赤道平面内的低轨道卫星b,地球的位置关系如图所示,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,且均绕地球同向运行,已知卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略,下列分析正确的是( )| A. | 卫星a、b的速度之比为2:1 | |
| B. | 卫星b星的周期为$\frac{T}{8}$ | |
| C. | 卫星b每次在盲区运行的时间为$\frac{{{θ_1}+{θ_2}}}{14π}T$ | |
| D. | 卫星a运行一周将于卫星b相距最近出现16次 |
4.在离地面高度为h处竖直向上抛出一质量为m的物体,抛出时的速度为v0,当它落到地面时的速度为v,用g表示重力加速度,则在此过程中空气阻力对物体做的功为( )
| A. | $mgh-\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2$ | B. | $\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2+mgh$ | ||
| C. | $mgh+\frac{1}{2}mv_0^2-\frac{1}{2}m{v^2}$ | D. | $\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2-mgh$ |
14.下列说法正确的是( )
| A. | 研究运动中的汽车车轮的转动快慢,车轮可看作质点 | |
| B. | 因为功和能的单位都是焦耳,所以功就是能 | |
| C. | 研究网球在空中飞行的轨迹,网球可看作质点 | |
| D. | 功是矢量,能是标量 |
1.下面说法错误的是( )
| A. | 海王星是人们依据万有引力定律计算出轨道而发现的 | |
| B. | 天王星是人们依据万有引力定律计算出轨道而发现的 | |
| C. | 天王星的运动轨道偏离根据万有引力定律计算出来的轨道,其原因是由 于天王星受到轨道外面其他行星的引力作用 | |
| D. | 冥王星是人们依据万有引力定律计算出轨道而发现的 |
18. 如图所示,M是一小型理想变压器,原副线圈匝数比为2:1,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,灯泡P上标有(110V,110W)的字样;开关闭合后,灯泡正常发光,电动机正常工作,若电动机的线圈电阻为2.5Ω,则以下说法中正确的是(g取10m/s2)( )
如图所示,M是一小型理想变压器,原副线圈匝数比为2:1,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,灯泡P上标有(110V,110W)的字样;开关闭合后,灯泡正常发光,电动机正常工作,若电动机的线圈电阻为2.5Ω,则以下说法中正确的是(g取10m/s2)( )
 如图所示,M是一小型理想变压器,原副线圈匝数比为2:1,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,灯泡P上标有(110V,110W)的字样;开关闭合后,灯泡正常发光,电动机正常工作,若电动机的线圈电阻为2.5Ω,则以下说法中正确的是(g取10m/s2)( )
如图所示,M是一小型理想变压器,原副线圈匝数比为2:1,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,灯泡P上标有(110V,110W)的字样;开关闭合后,灯泡正常发光,电动机正常工作,若电动机的线圈电阻为2.5Ω,则以下说法中正确的是(g取10m/s2)( )| A. | 开关闭合后,电压表的示数为100V,电流表的示数为2A | |
| B. | 开关闭合后,电源的输出功率为220W | |
| C. | 当用电动机匀速提起质量为10kg的重物时,重物上升的速度为10m/s | |
| D. | 某时刻电动机突然被卡住而停止转动,则电动机停转后灯泡可能被烧毁 |
19.下列说法正确的是( )
| A. | 雷达是用电磁波来测定物体位置的设备 | |
| B. | 电磁波可以通过电缆、光缆有线传输,也可以无线传输 | |
| C. | 眯着眼看发光的灯丝能观察到彩色条纹,这是光的偏振现象 | |
| D. | 电磁波和声波由空气进入水中传播时,其频率都不变,但波长和波速都变小 |