题目内容
如图所示,虚线上方有方向竖直向下的匀强电场,虚线上下有相同的匀强磁场,磁感应强度为B,方向垂直纸面向外,a b是一根长为 的绝缘细杆,沿电场线放置在虚线上方的场中,b端恰在虚线上,将一套在杆上的带正电的电量为q、质量为m的小球(小球重力忽略不计),从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
的绝缘细杆,沿电场线放置在虚线上方的场中,b端恰在虚线上,将一套在杆上的带正电的电量为q、质量为m的小球(小球重力忽略不计),从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是 /3,求:
/3,求:

①小球到达b点的速度vb;
②匀强电场的场强E;
③带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值.
【答案】
略
【解析】解: ①小球在磁场中作匀速圆周运动时,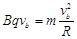
又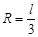 ∴vb=Bq
∴vb=Bq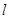 /3m
/3m
② 小球在沿杆向下运动时,受力情况如图,向左的洛仑兹力F,向右的弹力N,向下的电场力qE,向上的摩擦力f
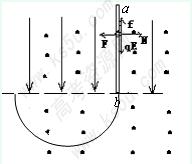
F=Bqvb,N=F=Bqvb ∴f=μN=μBqvb
当小球作匀速运动时,qE=f=μBqvb
E=B2ql/10m
③小球从a运动到b过程中,由动能定理得:

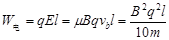
所以 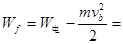
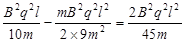
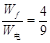

练习册系列答案
相关题目
 (2009?中山市模拟)如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上,将一套在杆上的带正电的小球从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
(2009?中山市模拟)如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上,将一套在杆上的带正电的小球从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是 如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,大小为B,方向垂直纸面向外,ab是一根长为L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上.将一套在杆上的带正电的轻小球,带电量为q,质量为m,从a端由静止释放,小球到达b端前已做匀速运动.已知小球与绝缘杆间的动摩擦因数为μ,小球重力忽略不计,当小球脱离杆进入虚线下方的磁场,求:
如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,大小为B,方向垂直纸面向外,ab是一根长为L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上.将一套在杆上的带正电的轻小球,带电量为q,质量为m,从a端由静止释放,小球到达b端前已做匀速运动.已知小球与绝缘杆间的动摩擦因数为μ,小球重力忽略不计,当小球脱离杆进入虚线下方的磁场,求: