题目内容
5. 如图所示,QA=3×10-8C,QB=-3×10-8C,A,B 两相距6cm,在水平方向外电场作用下,A,B保持静止,悬线竖直,则A,B连线中点场强大小5.25×105N/C,方向水平向右.(两带电小球可看作质点)
如图所示,QA=3×10-8C,QB=-3×10-8C,A,B 两相距6cm,在水平方向外电场作用下,A,B保持静止,悬线竖直,则A,B连线中点场强大小5.25×105N/C,方向水平向右.(两带电小球可看作质点)
分析 抓住A球平衡,根据点电荷的场强公式和匀强电场的定义式求出外电场的场强大小和方向;根据场强的叠加求出O点的合场强.
解答 解:悬线竖直,小球静止处于平衡状态,由平衡条件得:
对A球:EQA=k$\frac{{Q}_{A}{Q}_{B}}{{L}_{AB}^{2}}$,解得:E=7.5×104N/C,方向:水平向左;
点电荷在中点处产生的场强:EA=EB=k$\frac{{Q}_{A}}{(\frac{{L}_{AB}}{2})^{2}}$=$\frac{9×1{0}^{9}×3×1{0}^{-8}}{(\frac{0.06}{2})^{2}}$=3×105 N/C,
A、B在联系中点产生的场强方向都水平向右,
AB连线中点场强大小:E中=2EA-E=2×3×105-7.5×104=5.25×105N/C,方向:水平向右;
故答案为:5.25×105N/C;水平向右.
点评 本题考查了库仑定律以及场强的叠加,难度不大,知道场强是矢量,合场强等于各个场强的矢量和.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
13.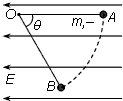 如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
 如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )| A. | 电场力与小球重力的关系是qE=mg | B. | 电场力与小球重力的关系是qE=$\sqrt{3}$mg | ||
| C. | 小球在B点时,细线拉力为FT=$\sqrt{3}$mg | D. | 小球在B点时,细线拉力为FT=$\frac{2\sqrt{3}}{3}$mg |
20.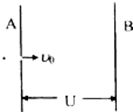 如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
 如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )| A. | 初速度为$\frac{{V}_{0}}{2}$,电压为$\frac{U}{2}$ | B. | 初速度为$\frac{{V}_{0}}{2}$,电压U不变 | ||
| C. | 初速度为V0,电压为$\frac{U}{2}$ | D. | 初速度为V0,电压为$\sqrt{2}$U |
17.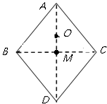 如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
 如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )| A. | A处与D处的场强相同 | |
| B. | 若再在A处固定电量为-Q的点电荷,则O处的场强大小为$\frac{9KQ}{{L}^{2}}$ | |
| C. | 若点电荷-Q从A静止释放,则经过M时速度最大 | |
| D. | 若点电荷+Q从B右侧靠近B的某点静止释放,沿BC向右运动过程加速度先增大后减小 |
14. 如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
 如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )| A. | 小球运动过程中机械能守恒 | |
| B. | 小球在轨道最低点时速度最大 | |
| C. | 小球在最低点对轨道的压力为mg+qE | |
| D. | 小球在最低点对轨道的压力为3(mg+qE) |
 如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨平面下水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻,有一匀强磁场垂直于导轨平面,磁感强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=1m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨平面下水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻,有一匀强磁场垂直于导轨平面,磁感强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=1m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8) 如图所示,倾角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接,轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T,匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=2T,现将两质量均为m=0.4kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放,g=10m/s2.
如图所示,倾角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接,轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T,匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=2T,现将两质量均为m=0.4kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放,g=10m/s2. 如图所示,用一根绝缘细线悬挂一个带电小球,小球的质量为m,电量为q,现加一水平的匀强电场,平衡时绝缘细线与竖直方向夹角为θ.
如图所示,用一根绝缘细线悬挂一个带电小球,小球的质量为m,电量为q,现加一水平的匀强电场,平衡时绝缘细线与竖直方向夹角为θ. 如图,平行板电容器AB间可看作匀强电场,电容C=1μF,场强E=1.2×102V/m,极板间距离d=5cm,电场中C和D分别到A、B两极板距离均为0.5cm.B极接地,求:?
如图,平行板电容器AB间可看作匀强电场,电容C=1μF,场强E=1.2×102V/m,极板间距离d=5cm,电场中C和D分别到A、B两极板距离均为0.5cm.B极接地,求:?