题目内容
4. 如图所示,为体验中心的“旋转飞人”项目,体验者在空中的运动可看作绳长为L的“圆锥摆”运动.质量为m的体验者在水平面内运动时
如图所示,为体验中心的“旋转飞人”项目,体验者在空中的运动可看作绳长为L的“圆锥摆”运动.质量为m的体验者在水平面内运动时细绳与竖直方向的夹角为θ,重力加速度为g,求该体验者:
(1)受到绳拉力的大小;
(2)受到向心力的大小;
(3)做匀速圆周运动的周期.
分析 (1)根据小球在竖直方向上的合力为零,求出绳子的拉力.
(2)绳子拉力在水平方向上的分力提供向心力,结合平行四边形定则求出向心力的大小.
(3)根据合力提供向心力求出匀速圆周运动的周期.
解答 解:(1)设绳中张力为FT,根据竖直方向上平衡有:FTcosθ=mg,
解得:${F_T}=\frac{mg}{cosθ}$.
(2)设向心力为F,则有:F=FTsinθ,
解得:F=mgtanθ.
(3)设周期为T,则有:$mgtanθ=mLsinθ{(\frac{2π}{T})^2}$
解得:$T=2π\sqrt{\frac{Lcosθ}{g}}$.
答:(1)受到绳拉力的大小为$\frac{mg}{cosθ}$;
(2)受到向心力的大小为mgtanθ;
(3)做匀速圆周运动的周期为$2π\sqrt{\frac{Lcosθ}{g}}$.
点评 本题是圆锥摆问题,由重力和绳子拉力的合力提供向心力,要注意圆周运动的圆心不是悬点,半径不是绳长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 一列水波通过某孔的实际情况如右图所示,现把孔的尺寸变小,或者把水波的波长变大,水波通过孔后的假想情况如下图所示,其假想正确的图示有( )
一列水波通过某孔的实际情况如右图所示,现把孔的尺寸变小,或者把水波的波长变大,水波通过孔后的假想情况如下图所示,其假想正确的图示有( )
 一列水波通过某孔的实际情况如右图所示,现把孔的尺寸变小,或者把水波的波长变大,水波通过孔后的假想情况如下图所示,其假想正确的图示有( )
一列水波通过某孔的实际情况如右图所示,现把孔的尺寸变小,或者把水波的波长变大,水波通过孔后的假想情况如下图所示,其假想正确的图示有( )| A. |  孔变小 | B. |  孔变小 | C. |  波长变大 | D. |  波长变大 |
15. 铁路在弯道处的内、外轨道高低是不同的,已知内、外轨道连线与水平面倾角为θ,弯道处的圆弧半径为R,若质量为m的火车转弯的时速度小于临界转弯速度$\sqrt{Rgtanθ}$时,则( )
铁路在弯道处的内、外轨道高低是不同的,已知内、外轨道连线与水平面倾角为θ,弯道处的圆弧半径为R,若质量为m的火车转弯的时速度小于临界转弯速度$\sqrt{Rgtanθ}$时,则( )
 铁路在弯道处的内、外轨道高低是不同的,已知内、外轨道连线与水平面倾角为θ,弯道处的圆弧半径为R,若质量为m的火车转弯的时速度小于临界转弯速度$\sqrt{Rgtanθ}$时,则( )
铁路在弯道处的内、外轨道高低是不同的,已知内、外轨道连线与水平面倾角为θ,弯道处的圆弧半径为R,若质量为m的火车转弯的时速度小于临界转弯速度$\sqrt{Rgtanθ}$时,则( )| A. | 内轨受挤压 | |
| B. | 外轨受挤压 | |
| C. | 这时铁轨对火车的支持力等于$\frac{mg}{cosθ}$ | |
| D. | 这时铁轨对火车的支持力小于$\frac{mg}{cosθ}$ |
12. 如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆的角速度为ω1时,小球旋转平面在A处,此时球对杆的压力设为FA;当杆角速度为ω2时,小球旋转平面在B处,设此时球对杆的压力为FB,则有( )
如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆的角速度为ω1时,小球旋转平面在A处,此时球对杆的压力设为FA;当杆角速度为ω2时,小球旋转平面在B处,设此时球对杆的压力为FB,则有( )
 如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆的角速度为ω1时,小球旋转平面在A处,此时球对杆的压力设为FA;当杆角速度为ω2时,小球旋转平面在B处,设此时球对杆的压力为FB,则有( )
如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆的角速度为ω1时,小球旋转平面在A处,此时球对杆的压力设为FA;当杆角速度为ω2时,小球旋转平面在B处,设此时球对杆的压力为FB,则有( )| A. | FA>FB | B. | FA=FB | C. | ω1<ω2 | D. | ω1>ω2 |
19.中国“北斗”卫星导航系统是我国自行研制的全球卫星定位与通信系统,是继美国GPS系统和俄罗斯“格洛纳斯”(GLONASS)系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30颗非地球同步卫星,以下说法正确的是( )
| A. | 这5颗地球同步卫星的运行速度大于第一宇宙速度 | |
| B. | 这5颗地球同步卫星的运行周期都与地球自转周期相等 | |
| C. | 这5颗地球同步卫星运动的加速度大小不一定相同 | |
| D. | 为避免相撞,不同国家发射的地球同步卫星必须运行在不同的轨道上 |
9.下列有关光的说法中正确的是( )
| A. | 光的干涉中也存在着光的衍射现象 | |
| B. | 泊松亮斑是光通过圆孔发生衍射时形成的 | |
| C. | 在岸边观察前方水中的一条鱼,鱼的实际深度要比看到的要深 | |
| D. | 眼睛通过一偏振片观察太阳,不停的转动偏振片,透射光亮度会发生改变 | |
| E. | 医学上用光导纤维制成内窥镜,用来检查人体内脏器官的内部,它利用了光的全反射原理 |
13.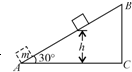 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 机械能损失了$\frac{1}{2}$mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了mgh | D. | 重力势能增加了$\frac{3}{4}$mgh |
 A、B两球沿同一条直线相向运动,所给的x-t图象记录了它们碰撞前后的运动情况,其中a和b分别为A、B碰撞前的x-t图象,c为碰撞后它们的x-t图象,若A球质量为3kg,根据图象可以求出B球质量是2kg;碰撞后损失的动能是15J.
A、B两球沿同一条直线相向运动,所给的x-t图象记录了它们碰撞前后的运动情况,其中a和b分别为A、B碰撞前的x-t图象,c为碰撞后它们的x-t图象,若A球质量为3kg,根据图象可以求出B球质量是2kg;碰撞后损失的动能是15J.