题目内容
12.在正、负电子对撞机中,一个负电子和一个正电子对撞发生湮灭而转化为一对光子.设正、负电子的静止质量均为m,对撞前的动能均为E,光在真空中的速度为c,普朗克常量为h,则对撞前后比较:(1)质量亏损△m=2m
(2)转化成光子在真空中的波长λ=$\frac{hc}{{E}_{k}+m{c}^{2}}$.
分析 光子无静止质量,根据反应前后质量之差求出质量亏损,由爱因斯坦质能方程求出电子对撞放出的能量,根据能量守恒定律求出光子具有的能量.由光子能量公式E=hγ,波速公式c=λγ求出光子的波长.
解答 解:(1)由于光子无静止的质量,则电子对撞过程中的质量亏损为:△m=2m-0=2m.
(2)由爱因斯坦质能方程中电子对撞放出的能量为△E=△mc2=2mc2,
根据能量守恒得,每个光子的能量为:E=$\frac{2m{c}^{2}+{2E}_{k}}{2}$=mc2+Ek,
又E=hγ=$\frac{hc}{λ}$,联立得到波长为:λ=$\frac{hc}{{E}_{k}+m{c}^{2}}$.
故答案为:(1)2m;(2)$\frac{hc}{{E}_{k}+m{c}^{2}}$.
点评 本题要知道光子的质量为零,运用能量守恒定律时,电子对撞前的动能不能忘记.

练习册系列答案
相关题目
3.设地球绕太阳近似作匀速圆周运动,已知轨道半径为R0,公转周期约为T0=365天;月球绕地球近似作匀速圆周运动,已知轨道半径为R,周期约为T=27.3天.另据勘测结果知道,在月球的永暗面存在着大量常年以固态形式蕴藏的水冰.根据天文观测,月球半径R月为1738km,地球半径R地约为6400km,月球表面的重力加速度约为地球表面的重力加速度的$\frac{1}{6}$,月球表面在阳光照射下的温度可达127℃,已知此温度下水蒸气分子的平均速率达到v0=2000m/s.已知万有引力常量为G,地球表面的重力加速度取g=10m/s2,则以下说法正确的是( )
| A. | 根据开普勒第三定律知:$\frac{{R}^{3}}{{T}^{2}}$=$\frac{{{R}_{0}}^{3}}{{{T}_{0}}^{2}}$ | |
| B. | 根据题给信息可知在月球表面暗面有冰,阳面有水 | |
| C. | 地心到月心之间的距离数量级为1010m | |
| D. | 根据题给数据和符号可以计算出太阳、地球、月球的质量 |
20.“用霍尔元件测量磁场”的实验中,把载流子为带负电的电子e的霍尔元件接入电路,如图甲所示,电流为I,方向向右,长方体霍尔元件长、宽、高分别为a=6.00mm、b=5.00mm、c=0.20mm,处于竖直向上的恒定匀强磁场中.
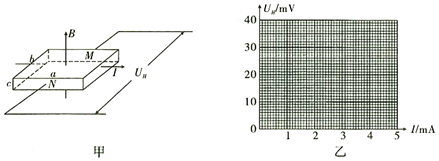
(1)前后极板M、N,电势较高的是M板(填“M板”或“N板”).
(2)某同学在实验时,改变电流的大小,记录了不同电流下对应的UH值,如下表:
请根据表格中的数据,在坐标乙中画出UH-I图象.已知该霍尔元件单位体积中自由载流子个数为n=6.25×1019m-3,则根据图象,由公式I=nebcv,可算出磁场B=0.016T(保留2位有效数字).
(3)有同学认为$\frac{{U}_{H}}{I}$代表了霍尔元件的电阻,请问这种想法正确吗?请说明理由:电流I不是由UH产生的.

(1)前后极板M、N,电势较高的是M板(填“M板”或“N板”).
(2)某同学在实验时,改变电流的大小,记录了不同电流下对应的UH值,如下表:
| I(mA) | 1.3 | 2.2 | 3.0 | 3.7 | 4.4 |
| UH (mV) | 10.2 | 17.3 | 23.6 | 29.1 | 34.6 |
(3)有同学认为$\frac{{U}_{H}}{I}$代表了霍尔元件的电阻,请问这种想法正确吗?请说明理由:电流I不是由UH产生的.
17.如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.监测到推力F、物体速度v随时间t变化的规律如图乙、丙所示.取g=10m/s2,则( )


| A. | 第1 s内推力做功为1 J | |
| B. | 第1.5 s时推力F的功率为2 W | |
| C. | 第2 s内物体克服摩擦力做的功为W=2.0 J | |
| D. | 第2 s内推力F做功的平均功率$\overline P$=1.5 W |
1.下列说法正确的是( )
| A. | 单晶体具有固定的熔点,多晶体没有固定的熔点 | |
| B. | 当物体的温度升高时,物体内所有分子的动能都增大 | |
| C. | 当分子间作用力表现为斥力时,分子势能随分子间距离的减小而增大 | |
| D. | 石墨层状结构间距较大,沿此方向易剥下,因而其机械强度有方向性 |
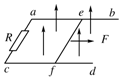 如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度.
如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度. 一个圆盘在水平面内匀速转动,角速度是5rad/s.盘面上距圆盘中心0.50m的位置有一个质量为0.10kg的小物体能够随圆盘一起=运动,如图所示,求:
一个圆盘在水平面内匀速转动,角速度是5rad/s.盘面上距圆盘中心0.50m的位置有一个质量为0.10kg的小物体能够随圆盘一起=运动,如图所示,求: 如图为某型号电风扇的铭牌,该电风扇工作时是利用交流电(选填“交流”或“直流”),该电风扇在额定电压工作一个小时消耗0.065度电能.
如图为某型号电风扇的铭牌,该电风扇工作时是利用交流电(选填“交流”或“直流”),该电风扇在额定电压工作一个小时消耗0.065度电能. 如图所示,将一个质量为m=2.0kg的闭合的矩形线圈abcd用两条绝缘的细线悬挂在天花板上的OO′两点上,两条细线竖直,线圈的ab边水平.线圈abcd的下部二分之一的区域有垂直于线圈平面的匀强磁场,磁感应强度的大小B=0.5T,矩形线圈的ab边长L1=0.5m,bc边长L2=0.4m,线圈匝数N=100匝,线圈总电阻为5Ω.求:
如图所示,将一个质量为m=2.0kg的闭合的矩形线圈abcd用两条绝缘的细线悬挂在天花板上的OO′两点上,两条细线竖直,线圈的ab边水平.线圈abcd的下部二分之一的区域有垂直于线圈平面的匀强磁场,磁感应强度的大小B=0.5T,矩形线圈的ab边长L1=0.5m,bc边长L2=0.4m,线圈匝数N=100匝,线圈总电阻为5Ω.求: