题目内容
3.“北斗”导航系统是我国自行研发的全球导航系统,它由5颗静止轨道卫星(同步卫星)与30颗非静止轨道卫星组成.已知月球公转周期约为27天,则静止轨道卫星与月球( )| A. | 角速度之比约为27:1 | B. | 线速度之比约为27:1 | ||
| C. | 半径之比约为1:27 | D. | 向心加速度之比约为1:27 |
分析 根据万有引力提供圆周运动向心力求出圆周运动的周期与半径的关系,周期与角速度关系,及周期与线速度的关系,从而确定向心加速度关系.
解答 解:A、根据$ω=\frac{2π}{T}$,可知,角速度与周期成反比,因静止轨道卫星与月球的公转周期之比为1:27,则角速度之比约为27:1,故A正确;
BC、根据万有引力提供圆周运动向心力有:$\frac{GMm}{{r}^{2}}$=$\frac{m•4{π}^{2}r}{{T}^{2}}$
得卫星运动的周期T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
可得月球周期与同步卫星周期的比值:$\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{{r}_{1}^{3}}{{r}_{2}^{3}}}$
所以月球到地球的距离与同步卫星到地球的距离比为:$\frac{{r}_{1}}{{r}_{2}}$=($\frac{27}{1}$)${\;}^{\frac{2}{3}}$=$\frac{9}{1}$
即同步卫星到地球的距离与月球到地球的距离比为1:9;
再根据$v=\frac{2πr}{T}$,即得线速度之比约为3:1,故BC错误;
D、根据an=vω,得向心加速度之比约为81:1,故D错误;
故选:A.
点评 根据万有引力提供圆周运动向心力并由此根据周期关系求半径关系,再求得线速度、角速度,及向心加速度的关系,掌握规律并能灵活应用规律是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.
在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.
已知重力加速度g=9.8m/s2,要求尽可能多的利用测量数据,计算弹簧甲的劲度系数k=100N/m(保留三位有效数字).由表中数据能(填“能”或“不能”)计算弹簧乙的原长.
 在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.
在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.| 钩码个数 | 1 | 2 | 3 | 4 |
| L1/cm | 26.00 | 26.48 | 26.97 | 27.47 |
| L2/cm | 79.44 | 80.89 | 82.36 | 83.85 |
8. 如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )
如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )
 如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )
如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )| A. | 该粒子一定带负电 | B. | 该粒子达到点B时的动能为40eV | ||
| C. | 改变初速度方向,该粒子可能经过C | D. | 改变初速度方向,该粒子可能经过D |
14. 2013年6月11日,“神舟十号”飞船发射成功,“神舟十号”与“天宫一号”对接前按如图所示的轨道示意图运行,下列说法中正确的是( )
2013年6月11日,“神舟十号”飞船发射成功,“神舟十号”与“天宫一号”对接前按如图所示的轨道示意图运行,下列说法中正确的是( )
 2013年6月11日,“神舟十号”飞船发射成功,“神舟十号”与“天宫一号”对接前按如图所示的轨道示意图运行,下列说法中正确的是( )
2013年6月11日,“神舟十号”飞船发射成功,“神舟十号”与“天宫一号”对接前按如图所示的轨道示意图运行,下列说法中正确的是( )| A. | “神舟十号”的周期比“天宫一号”小 | |
| B. | “神舟十号”的速度比“天宫一号”小 | |
| C. | “神舟十号”的角速度比“天宫一号”小 | |
| D. | “神舟十号”的加速度比“天宫一号”小 |

 如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无滑动,大轮的半径是小轮的2倍,大轮上的一点S离转动轴的距离是大轮半径的0.5倍,当大轮边缘上P点的向心加速度是10m/s2时,大轮上的S点和小轮上的Q点的向心加速度分别为aS=5m/s2,aQ=20m/s2.
如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无滑动,大轮的半径是小轮的2倍,大轮上的一点S离转动轴的距离是大轮半径的0.5倍,当大轮边缘上P点的向心加速度是10m/s2时,大轮上的S点和小轮上的Q点的向心加速度分别为aS=5m/s2,aQ=20m/s2. 如图所示,长L=1m的小车静止在光滑的水平面上,一滑块以v0=3m/s的水平
如图所示,长L=1m的小车静止在光滑的水平面上,一滑块以v0=3m/s的水平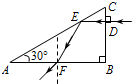 如图所示,直角棱镜ABC置于空气中,∠A=30°,AB边长为2a.一束单色光从D点垂直于BC边射入棱镜,在AC边上的E点恰好发生一次全反射后,从AB边中点F处射出.已知真空中光速为c.求:
如图所示,直角棱镜ABC置于空气中,∠A=30°,AB边长为2a.一束单色光从D点垂直于BC边射入棱镜,在AC边上的E点恰好发生一次全反射后,从AB边中点F处射出.已知真空中光速为c.求: 一定质量的理想气体,由状态A通过如图所示的箭头方向变化到状态C.则气体由状态A到状态B的过程中,气体的内能不变(选填“增大”、“减小”或“不变”),气体由状态A到状态C的过程中,气体与外界总的热交换情况是放热(选填“吸热”、“放热”或“无法确定”)
一定质量的理想气体,由状态A通过如图所示的箭头方向变化到状态C.则气体由状态A到状态B的过程中,气体的内能不变(选填“增大”、“减小”或“不变”),气体由状态A到状态C的过程中,气体与外界总的热交换情况是放热(选填“吸热”、“放热”或“无法确定”)