题目内容
7.如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.(1)求匀强电场的电场强度E;
(2)求在AC间还有哪些位置的粒子,通过电场后也能沿x轴正方向运动?
(3)若以直线x=2l0上的某点为圆心的圆形区域内,分布着垂直于xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点处,而便于被收集,则磁场区域的最小半径是多大?相应的磁感应强度B是多大?

分析 (1)将带电粒子的运用沿水平和竖直方向正交分解,水平方向做匀速直线运动,竖直方向在x轴上下方都做匀变速直线运动,根据牛顿第二定律和运动学公式列式分析;
(2)先画出运动的一般轨迹,要使粒子通过电场后能沿x轴正方向运动,其第一次到达x轴的水平分位移的2n倍等于2l0,根据牛顿第二定律和运动学公式列式分析即可;
(3)先画出各个粒子的运动轨迹,然后根据题意确定磁场范围,最后根据洛伦兹力提供向心力求解磁感应强度.
解答 解:(1)从A点射出的粒子,由A到A′的运动时间为T,根据运动轨迹和对称性可得
x轴方向 $2{l}_{0}^{\;}={v}_{0}^{\;}T$
y轴方向 $2{l}_{0}^{\;}=\frac{1}{2}\frac{qE}{m}(\frac{T}{2})_{\;}^{2}×2$
得:$E=\frac{2m{v}_{0}^{2}}{q{l}_{0}^{\;}}$
(2)设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向,粒子第一次达x轴用时△t,水平位移为△x,则
$△x={v}_{0}^{\;}△t$
$△y=\frac{1}{2}\frac{qE}{m}(2△t)_{\;}^{2}$
若满足$2{l}_{0}^{\;}=n•2△x$,则从电场射出时的速度方向也将沿x轴正方向
解之得:$△y=\frac{1}{{n}_{\;}^{2}}\frac{1}{2}\frac{qE}{m}(\frac{{l}_{0}^{\;}}{{v}_{0}^{\;}})_{\;}^{2}=\frac{1}{{n}_{\;}^{2}}{l}_{0}^{\;}$
即AC间y坐标为$y=(-1)_{\;}^{n}\frac{1}{{n}_{\;}^{2}}{l}_{0}^{\;}$(n=1,2,3,…)
(3)当n=1时,粒子射出的坐标为${y}_{1}^{\;}={l}_{0}^{\;}$
当n=2时,粒子射出的坐标为${y}_{2}^{\;}=-\frac{1}{4}{l}_{0}^{\;}$
当n≥3时,沿x轴正方向射出的粒子分布在y1到y2之间(如图)y1到y2之间的距离为
L=y1-y2=$\frac{5}{4}{l}_{0}^{\;}$ 则磁场的最小半径为 $R=\frac{L}{2}=\frac{5{l}_{0}^{\;}}{8}$
若使粒子经磁场偏转后汇聚于一点,粒子的运动半径与磁场圆的半径相等(如图),(轨迹圆与磁场圆相交,四边形PO1QO2为棱形)
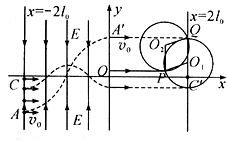
由$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{R}$
得:$B=\frac{8m{v}_{0}^{\;}}{5q{l}_{0}^{\;}}$
答:(1)求匀强电场的电场强度E为$\frac{2m{v}_{0}^{2}}{q{l}_{0}^{\;}}$;
(2)在AC间的粒子位置满足$y=(-1)_{\;}^{n}\frac{1}{{n}_{\;}^{2}}{l}_{0}^{\;}$(n=1、2、3…),通过电场后也能沿x轴正方向运动
(3)若以直线x=2l0上的某点为圆心的圆形区域内,分布着垂直于xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点处,而便于被收集,则磁场区域的最小半径是$\frac{5}{8}{l}_{0}^{\;}$,相应的磁感应强度B是$\frac{8m{v}_{0}^{\;}}{5q{l}_{0}^{\;}}$
点评 本题关键是将粒子的运动沿着水平方向和竖直方向正交分解,然后根据牛顿运动定律和运动学公式列式分析求解;解题过程中要画出轨迹图分析,特别是第三小题,要画出准确的圆轨迹图分析才能有助与问题的解决.

| A. | 电场强度为零的地方,电势一定为零 | |
| B. | 电场是一种客观存在,具有能量和动量 | |
| C. | 电荷在电场中某点的受力方向即为该点的电场强度的方向 | |
| D. | 电场强度大的地方,电场线一定密,电势也一定高 |
 如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )
如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )| A. | 恒力F可能沿与水平方向夹30°斜向右下的方向 | |
| B. | 当小圆环在直杆上运动的时间最短时,小圆环与直杆间必无挤压 | |
| C. | 若恒力F的方向水平向右,则恒力F的大小为$\sqrt{3}$mg | |
| D. | 恒力F的最小值为$\frac{\sqrt{3}}{2}$mg |
 如图所示,虚线a、b、c为电场中的三个等势面,实线是等势面的对称轴,A、B、C分别是实线与三个等势面的交点,D、E分别是AB和BC的中点,a的电势为φ0,相邻等势面间的电势差相等,一带电量为-q的粒子由A点静止释放,只在电场力的作用下运动,到C点时的动能为EK,则( )
如图所示,虚线a、b、c为电场中的三个等势面,实线是等势面的对称轴,A、B、C分别是实线与三个等势面的交点,D、E分别是AB和BC的中点,a的电势为φ0,相邻等势面间的电势差相等,一带电量为-q的粒子由A点静止释放,只在电场力的作用下运动,到C点时的动能为EK,则( )| A. | 粒子在运动过程中的加速度不断减小 | |
| B. | 粒子到B点的动能为$\frac{1}{2}$ EK | |
| C. | 等势面B的电势为φ0-$\frac{{E}_{K}}{2q}$ | |
| D. | UCE>UDA |
 某实验小组利用力传感器和光电门传感器探究“动能定理”.将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小.在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图所示.在小车上放置砝码来改变小车质量,用不同的重物G来改变拉力的大小,摩擦力不计.
某实验小组利用力传感器和光电门传感器探究“动能定理”.将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小.在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图所示.在小车上放置砝码来改变小车质量,用不同的重物G来改变拉力的大小,摩擦力不计.(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1,把细线的一端固定在力传感器上,另一端通过定滑轮与重物G相连,正确连接所需电路;
②将小车停在点C,由静止开始释放小车,
| 次数 | M/kg | |v22-v12|/m2s-2 | △E/J | F/N | W/J |
| 1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | △E3 | 1.22 | W3 |
| 4 | 1.00 | 2.40 | 1.20 | 2.42 | 1.21 |
| 5 | 1.00 | 2.84 | 1.42 | 2.86 | 1.43 |
③改变小车的质量或重物的质量,重复②的操作.
(2)右侧表格中M是M1与小车中砝码质量之和,△E为动能变化量,F是拉力传感器的拉力,W是F在A、B间所做的功.表中的△E3=0.600J,W3=0.610J(结果保留三位有效数字).

(1)某同学用游标卡尺测量遮光条的宽度d,如图乙所示,则d=2.30mm.
(2)下列实验要求中不必要的一项是A(请填写选项前对应的字母).
A.应使滑块质量远大于钩码和力传感器的总质量
B.应使A位置与光电门间的距离适当大些
C.应将气垫导轨调至水平
D.应使细线与气垫导轨平行
(3)实验时保持滑块的质量M和A、B间的距离L不变,改变钩码质量m,测出对应的力传感器的示数F和遮光条通过光电门的时间t,通过描点作出线性图象,研究滑块动能变化与合外力对它所做功的关系,处理数据时应作出的图象是C(请填写选项前对应的字母).
| A.作出“t-F图象” | B.作出“t2-F图象” |
| C.作出“t2-$\frac{1}{F}$图象” | D.作出“$\frac{1}{t}$-F2图象” |


 如图所示,一倾角为θ=37°的斜面上放有一足够长的木板B,B的右端放一体积可忽略不计的物块A,己知mA=1kg,mB=4kg,A与B的动摩擦因数μ1=$\frac{7}{8}$,B与斜面间的动摩擦因数μ2=$\frac{1}{40}$,最大静摩擦力等于滑动摩擦力,(取g=10m/s2,sin37°=0.6)求:
如图所示,一倾角为θ=37°的斜面上放有一足够长的木板B,B的右端放一体积可忽略不计的物块A,己知mA=1kg,mB=4kg,A与B的动摩擦因数μ1=$\frac{7}{8}$,B与斜面间的动摩擦因数μ2=$\frac{1}{40}$,最大静摩擦力等于滑动摩擦力,(取g=10m/s2,sin37°=0.6)求: