题目内容
图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向,磁分析器中与O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,磁感应强度为B,其左边界与静电分析器的右端面平行.由离子源发出的正离子(初速度为0,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为d.求:(1)离子的比荷q/m.
(2)静电分析器中离子运动轨迹处电场强度E的大小.
(3)现将离子换成质量不同的另一种正离子,其它条件不变.该离子进入磁分析器后,它射出磁场的位置在Q点的左侧,离子的质量与原来相比是增大还是减小?

【答案】分析:(1)根据动能定理求出带电粒子射出加速电场时的速度,带电粒子在静电分析器中做匀速圆周运动,在磁分析器中做匀速圆周运动,根据半径公式求出离子的比荷.
(2)粒子在静电分析器中做匀速圆周运动,靠电场力提供向心力,根据牛顿第二定律求出电场强度的大小.
(3)离子在加速电场中加速后,进入静电分析器中做匀速圆周运动,结合动能定理和牛顿第二定律发现,轨道半径与离子的质量、电量无关,进入磁分析器中靠洛伦兹力提供向心力,通过半径的变化判断质量的变化.
解答:解:(1)根据qU=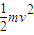 ,解得v=
,解得v=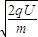 .
.
由qvB=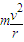 ,r=d.
,r=d.
解得d=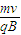 .
.
所以比荷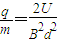 .
.
(2)根据牛顿第二定律有:qE=m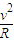 ,
,
解得:E=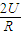 .
.
(3)由qE=m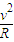 ,qU=
,qU=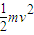 ,知带电粒子在静电分析器中做匀速圆周运动,轨道半径与离子的质量、电量无关.
,知带电粒子在静电分析器中做匀速圆周运动,轨道半径与离子的质量、电量无关.
在磁分析器中有:qvB=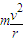 ,qU=
,qU=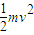 ,
,
联立两式解得:r=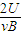 =
=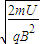 .半径减小,知离子质量减小.
.半径减小,知离子质量减小.
答:(1)离子的比荷为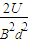 .
.
(2)静电分析器中离子运动轨迹处电场强度E的大小为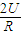 .
.
(3)离子进入磁分析器后,它射出磁场的位置在Q点的左侧,离子的质量与原来相比减小.
点评:解决本题的关键知道离子在加速电场,静电分析器和磁分析器中的运动规律,结合牛顿第二定律和动能定理进行求解.
(2)粒子在静电分析器中做匀速圆周运动,靠电场力提供向心力,根据牛顿第二定律求出电场强度的大小.
(3)离子在加速电场中加速后,进入静电分析器中做匀速圆周运动,结合动能定理和牛顿第二定律发现,轨道半径与离子的质量、电量无关,进入磁分析器中靠洛伦兹力提供向心力,通过半径的变化判断质量的变化.
解答:解:(1)根据qU=
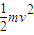 ,解得v=
,解得v=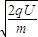 .
.由qvB=
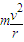 ,r=d.
,r=d.解得d=
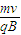 .
.所以比荷
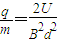 .
.(2)根据牛顿第二定律有:qE=m
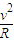 ,
,解得:E=
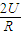 .
.(3)由qE=m
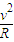 ,qU=
,qU=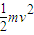 ,知带电粒子在静电分析器中做匀速圆周运动,轨道半径与离子的质量、电量无关.
,知带电粒子在静电分析器中做匀速圆周运动,轨道半径与离子的质量、电量无关.在磁分析器中有:qvB=
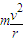 ,qU=
,qU=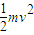 ,
,联立两式解得:r=
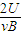 =
=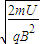 .半径减小,知离子质量减小.
.半径减小,知离子质量减小.答:(1)离子的比荷为
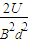 .
.(2)静电分析器中离子运动轨迹处电场强度E的大小为
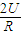 .
.(3)离子进入磁分析器后,它射出磁场的位置在Q点的左侧,离子的质量与原来相比减小.
点评:解决本题的关键知道离子在加速电场,静电分析器和磁分析器中的运动规律,结合牛顿第二定律和动能定理进行求解.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 (2011?南充二模)图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向,磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面的匀强磁场,其左边界与静电分析器的右端面平行.由离子源发出的一质量为m、电荷量为q的正离子(初速度为零,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为么求:
(2011?南充二模)图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向,磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面的匀强磁场,其左边界与静电分析器的右端面平行.由离子源发出的一质量为m、电荷量为q的正离子(初速度为零,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为么求: (2011?万州区模拟)图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向,磁分析器中与O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,磁感应强度为B,其左边界与静电分析器的右端面平行.由离子源发出的正离子(初速度为0,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为d.求:
(2011?万州区模拟)图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向,磁分析器中与O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,磁感应强度为B,其左边界与静电分析器的右端面平行.由离子源发出的正离子(初速度为0,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为d.求: 有一种“双聚焦分析器”质谱仪,工作原理如图所示.加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为
有一种“双聚焦分析器”质谱仪,工作原理如图所示.加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为
